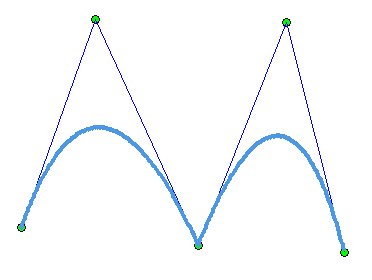
B 样条曲线是在 Bezier 曲线基础上发展起来的一类曲线，它客服了 Bezier 曲线整体控制性所带来的不便，最常用的是二次与三次 B 样条曲线。

1 什么是样条

样条（spline）二字，是从英文翻译过来的。

  • 实际应用中，样条是一根富有弹性的细木条或塑料条。在应用 CAD/CAM 技术以前，航空、船舶和汽车制造业普遍采用手工绘制自由曲线。绘图时用压铁使样条通过指定的形值点（样点），再适当地调整压铁，改变样条形态，直到符合设计要求。所以在绘图术语中，样条是通过一组指定点集而生成平滑曲线的柔性带。样条曲线（spline curve）原指用这种方式绘制的曲线。
  • 从力学角度考虑，样条可看做一弹性细梁，压铁是作用在梁上的集中载荷。由此，设计样条曲线的过程可抽象为：求弹性细梁在外加集中载荷作用下产生的弯曲变形。
  • 在数学上使用分段的三次多项式函数来描绘这种曲线，其中各曲线段的连接处有连续的一次和二次导数。
  • 在计算机图形学中，样条曲线指由多项式曲线段连接而成的曲线，在每段的边界处满足特定的连续性条件。

2 Bezier 曲线

2.1 Bezier 曲线介绍

贝塞尔曲线是这样的一条曲线，它是依据四个位置任意的点坐标绘制出的一条光滑曲线。在历史上，研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。1962 年，法国数学家 Pierre Bézier 第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名是为贝塞尔曲线。

2.2 Bezier 曲线定义

给定空间n+1个控制顶点$P_{i}(i=0 \rightarrow n)$，则 Bezier 曲线定义为： $$ p(t)= \sum_{i=1}^{n} P_{i}B_{i,n}(t) \qquad i \in [0,1] $$ 其中：$B_{i,n}(t)$称为基函数 $$ B_{i,n}(t)=\frac{n!}{i!(n-i)!}t^{i}(1-t)^{n-i}=C_{n}^{i}t^{i}(1-t)^{n-i} $$

2.3 Bezier 曲线性质

  • 端点性质：

    a) $p(0)=P_{0},p(1)=P_{n}$，即曲线过而二端点；

    b) $p'(0)=n(P_{1}-P_{0}),p'(1)=n(P_{n}-P_{n-1})$，即在二端点与控制多边形相切。

  • 凸包性：Bezier 曲线完成落在控制多边形的凸包内。

  • 对称性：由$P_{i}$与$P_{n-i}$组成的曲线,位置一致，方向相反。

  • 几何不变性：Bezier 曲线的形状仅仅与控制多边形各个顶点的相对位置有关，而与坐标系的选择无关。

  • 变差缩减性：若 Bezier 曲线的特征多边形是一个平面图形，则平面内任意直线与$p(t)$的交点个数不多于该直线与其特征多边形的交点个数，这一性质叫做变差缩减性质。

    此性质反应了 Bezier 曲线 比其特征多边形的波动还小，也就是说Bezier 曲线比特征多边形的折线更光顺。

Bezier 曲线的递推公式（de Casteljau 算法） $$ \begin{equation} P_{i}^{k} = \begin{cases} P_{i} & k=0 \\
(1-t)P_{i}^{k-1} + tP_{i+1}^{k-1} & k=1,2,…,n \quad i=0,1,…,n-k \end{cases} \end{equation} $$ de Casteljau 算法稳定可靠，直观简便，可以编出十分简便的程序，是计算 Bezier 曲线的基本算法和标准算法。

2.4 Bezier 曲线缺点

Bezier 曲线在外形设计的应用中存在一些具体的不足之处。主要有一下三点：

  • 确定了多边形的顶点数（n个），也就决定了所定义的Bezier曲线的阶次（n-1次），这样很不灵活；
  • 当顶点数（n）较大时，曲线的阶次将比较高。此时，多边形对曲线形状的控制将明显减弱；
  • Bezier 的调和函数的值，在开区间$(0,1)$内均不为0。因此，所定义的曲线在$(0<t<1)$的区间内的任何一点均要受到全部顶点的影响，即改变其中任一个顶点的位置，都将对整条曲线产生影响，因此对曲线进行局部修改是不可能的。

3 B 样条曲线

为了克服在 Bezier 曲线中存在的问题，Gordon、Riesenfeld 和 Forrest 等人拓展了 Bezier 曲线，用 n 次 B 样条基函数替换了伯恩斯坦基函数，构造了 B 样条曲线。B样条曲线除了保持 Bezier 曲线所具有的优点外，还增加了可以对曲线进行局部修改这一突出的优点。除此之外，它还具有对特征多边形更逼近以及多项式阶次较低等优点。因此，B 样条曲线在外形设计中得到了更广泛的重视和应用。

3.1 B 样条曲线定义

B 样条曲线方程可写为： $$ p(u)=\sum_{i=0}^{n}P_{i}N_{i,k}(u) $$ 其中，$P_{i}(i=0 \rightarrow n )$为控制顶点（坐标），$N_{i,k}(i=0 \rightarrow n)$为$k$次规范B样条基函数，最高次数为$k$。基函数是由一个节点矢量的非递减参数$u$的序列$U:u_{0} \leq u_{1} \leq … \leq u_{n+k+1}$所决定的$k$次多项式。

B 样条的基函数通常采用Cox-deBoor递推公式：

$$ \begin{cases} N_{i,0}(u)=\begin{cases} 1 & \mbox{if } u_{i} \leq u \leq u_{i+1} \\
0 & \mbox{others} \end{cases} \\
N_{i,k}(u)=\frac{u-u_{i}}{u_{i+k}-u_{i}}N_{i,k-1}(u)+\frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}N_{i+1,k-1}(u) \\
\mbox{define } \frac{0}{0} = 0 \end{cases} $$ 上式中，$i$为节点序号，$k$为基函数的次数，共有$n+1$个控制点。注意区分节点和控制顶点，节点是在节点矢量$U$中取得，控制顶点则是坐标点，决定B样条的控制多边形。Cox-deBoor递推公式是B样条曲线的定义的核心，该部分在程序中实现可采用递归的方式。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

% BaseFunction.m文件
function Nik_u = BaseFunction(i, k , u, NodeVector)
% 计算基函数Ni,k(u),NodeVector为节点向量

if k == 0       % 0次B样条
    if (u >= NodeVector(i+1)) && (u < NodeVector(i+2))
        Nik_u = 1.0;
    else
        Nik_u = 0.0;
    end
else
    Length1 = NodeVector(i+k+1) - NodeVector(i+1);
    Length2 = NodeVector(i+k+2) - NodeVector(i+2);      % 支撑区间的长度
    if Length1 == 0.0       % 规定0/0 = 0
        Length1 = 1.0;
    end
    if Length2 == 0.0
        Length2 = 1.0;
    end
    Nik_u = (u - NodeVector(i+1)) / Length1 * BaseFunction(i, k-1, u, NodeVector) ...
        + (NodeVector(i+k+2) - u) / Length2 * BaseFunction(i+1, k-1, u, NodeVector);
end

所给程序可用于计算基函数$N_{i,k}(u)$的值，程序中对不同类型的B样条曲线区别在于节点矢量 NodeVector 的取值不同。

3.2 B样条曲线的分类

根据节点矢量中节点的分布情况不同，可以划分4种类型的B样条曲线。不同类型的B样条曲线区别主要在于节点矢量，对于具有$n+1$个控制顶点$(P_{0},P_{1},…,P_{n})$的 $k $次B样条曲线，无论是哪种类型都具有$n+k+2$个节点$[u_{0},u_{1},…,u_{n+k+2}]$。

  • 均匀B样条曲线

    节点矢量中节点为沿参数轴均匀或等距分布。

  • 准均匀B样条曲线

    其节点矢量中两端节点具有重复度$k+1$，即$u_{0}=u_{1}=…=u_{k}$，$u_{n+1}=u_{n+2}=…=u_{n+k+1}$，所有的内节点均匀分布，具有重复度1。

  • 分段Bezier曲线

    其节点矢量中两端节点的重复度与类型2相同，为$k+1$。不同的是内节点重复度为$k$。该类型有限制条件，控制顶点数减1必须等于次数的正整数倍，即$\frac{n}{k}=正整数$。

  • 一般非均匀B样条曲线

    对任意分布的节点矢量$U=[u_{0},u_{1},…,u_{n+k+1}]$，只要在数学上成立都可选取。

3.3 B 样条曲线的绘制

3.3.1 节点矢量的确定

不同类型的 B 样条曲线区别主要在于节点矢量，对于具有$n+1$个控制顶点$(P_{0},P_{1},…,P_{n})$的 $k$ 次B样条曲线，无论是哪种类型都具有$n+k+2$个节点$([u_{0},u_{1}…u_{n+k+1}])$。

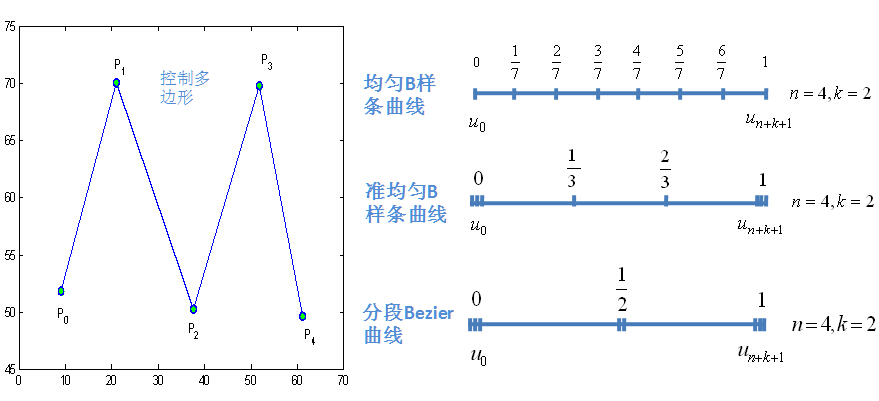
20150510153754214

根据图示，三种类型的B样条曲线对应的节点矢量分别为： $$ [0 \ \frac{1}{7} \ \frac{2}{7} \ \frac{3}{7} \ \frac{4}{7} \ \frac{5}{7} \ \frac{6}{7} \ 1] \\
[0 \ 0 \ 0 \ \frac{1}{3} \ \frac{2}{3} 1 \ 1 \ 1] \\
[0 \ 0 \ 0 \ \frac{1}{2} \ \frac{1}{2} 1 \ 1 \ 1] $$ 需要注意的是分段Bezier曲线必须满足$\frac{n}{k}=正整数$。

这里给出准均匀B样条和分段Bezier曲线的生成节点矢量的代码，均匀B样条的很简单就不列出了。假设共n+1个控制顶点，k次B样条，输入参数为 n, k ，输出节点矢量NodeVector。

准均匀B样条曲线的节点矢量生成：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

% U_quasi_uniform.m文件
function NodeVector = U_quasi_uniform(n, k)
% 准均匀B样条的节点向量计算，共n+1个控制顶点，k次B样条
NodeVector = zeros(1, n+k+2);
piecewise = n - k + 1;       % 曲线的段数
if piecewise == 1       % 只有一段曲线时，n = k
    for i = n+2 : n+k+2
        NodeVector(1, i) = 1;
    end
else
    flag = 1;       % 不止一段曲线时
    while flag ~= piecewise
        NodeVector(1, k+1+flag) = NodeVector(1, k + flag) + 1/piecewise;
        flag = flag + 1;
    end
    NodeVector(1, n+2 : n+k+2) = 1;
end

分段Bezier曲线的节点矢量生成：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

% U_piecewise_Bezier.m文件
function NodeVector = U_piecewise_Bezier(n, k)
% 分段Bezier曲线的节点向量计算，共n+1个控制顶点，k次B样条
% 分段Bezier端节点重复度为k+1，内间节点重复度为k,且满足n/k为正整数

if ~mod(n, k) && (~mod(k, 1) && k>=1)   % 满足n是k的整数倍且k为正整数
    NodeVector = zeros(1, n+k+2);   % 节点矢量长度为n+k+2
    NodeVector(1, n+2 : n+k+2) = ones(1, k+1);  % 右端节点置1

    piecewise = n / k;      % 设定内节点的值
    Flg = 0;
    if piecewise > 1
        for i = 2 : piecewise
            for j = 1 : k
                NodeVector(1, k+1 + Flg*k+j) = (i-1)/piecewise;
            end
            Flg = Flg + 1;
        end
    end

else
    fprintf('error!\n');
end

3.3.2 B样条曲线的绘制

根据B样条曲线的定义公式，曲线上任一点坐标值是参数变量$u$的函数，用矩阵形式表示 $$ p(u)=(P_{0} \quad P_{1} \quad … \quad P_{n} )\begin{pmatrix} (N_{0,k} (u) \\
(N_{1,k} (u) \\
\vdots \\
(N_{n,k} (u) \end{pmatrix} $$ 只需要确定控制顶点$d_{i}$、曲线的次数$k$ 以及基函数$N_{i,k}(u)$，就完全确定了曲线。

B样条曲线的绘制函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

% DrawSpline.m文件
function DrawSpline(n, k, P, NodeVector)
% B样条的绘图函数
% 已知n+1个控制顶点P(i), k次B样条，P是2*(n+1)矩阵存控制顶点坐标, 节点向量NodeVector
plot(P(1, 1:n+1), P(2, 1:n+1),...
                    'o','LineWidth',1,...
                    'MarkerEdgeColor','k',...
                    'MarkerFaceColor','g',...
                    'MarkerSize',6);
line(P(1, 1:n+1), P(2, 1:n+1));
Nik = zeros(n+1, 1);
for u = 0 : 0.005 : 1-0.005
    for i = 0 : 1 : n
        Nik(i+1, 1) = BaseFunction(i, k , u, NodeVector);
    end
    p_u = P * Nik;
    if u == 0
        tempx = p_u(1,1);
        tempy = p_u(2,1);
        line([tempx p_u(1,1)], [tempy p_u(2,1)],...
            'Marker','.','LineStyle','-', 'Color',[.3 .6 .9], 'LineWidth',3);
    else
        line([tempx p_u(1,1)], [tempy p_u(2,1)],...
            'Marker','.','LineStyle','-', 'Color',[.3 .6 .9], 'LineWidth',3);
        tempx = p_u(1,1);
        tempy = p_u(2,1);
    end
end

调用 DrawSpline(n, k, P, NodeVector) 函数就能绘制曲线，注意输入变量要正确。

下面给出绘制三种不同B样条曲线的命令流，可以参考比较每种类型之间的区别。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

% 绘制三种类型的B样条曲线，需要前面所给的所有.m文件
clear all;
%控制顶点
P = [9.036145, 21.084337, 37.607573, 51.893287, 61.187608;
    51.779661, 70.084746, 50.254237, 69.745763, 49.576271];

n = 4; k = 2;

flag = 2;
% flag = 1，绘制均匀B样条曲线
% flag = 2, 绘制准均匀B样条曲线
% flag = 3, 绘制分段Bezier曲线

switch flag
    case 1
        NodeVector = linspace(0, 1, n+k+2); % 均匀B样条的节点矢量

        % 绘制样条曲线
        plot(P(1, 1:n+1), P(2, 1:n+1),...
                        'o','LineWidth',1,...
                        'MarkerEdgeColor','k',...
                        'MarkerFaceColor','g',...
                        'MarkerSize',6);
        line(P(1, 1:n+1), P(2, 1:n+1));
        Nik = zeros(n+1, 1);
        for u = k/(n+k+1) : 0.001 : (n+1)/(n+k+1)
            % for u = 0 : 0.005 : 1
            for i = 0 : 1 : n
                Nik(i+1, 1) = BaseFunction(i, k , u, NodeVector);
            end
        p_u = P * Nik;
        line(p_u(1,1), p_u(2,1), 'Marker','.','LineStyle','-', 'Color',[.3 .6 .9]);
        end
    case 2
        NodeVector = U_quasi_uniform(n, k); % 准均匀B样条的节点矢量
        DrawSpline(n, k, P, NodeVector);
    case 3
        NodeVector = U_piecewise_Bezier(n, k);  % 分段Bezier曲线的节点矢量
        DrawSpline(n, k, P, NodeVector);
    otherwise
        fprintf('error!\n');
end

三种类型的B样条曲线

  • 均匀B样条曲线

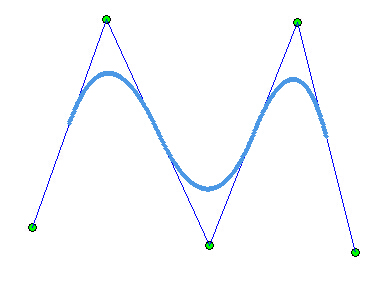
    20150510172723541

  • 准均匀B样条曲线

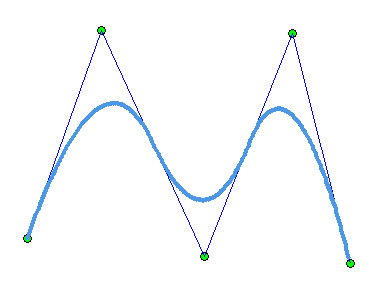
    20150510173020071

  • 分段Bezier曲线

    20150510172707221

参考文献

[1] https://blog.csdn.net/Mr_Grit/article/details/45603627