0 复习

机器人学基础知识已经完成第8篇了，这里梳理下：

1 逆运动学（Inverse Kinematics）

有了前面的铺垫，理解逆运动学所研究的问题就变得非常简单了——我要求我的end effector运动到某一个位置朝向某一个方向（比如我要控制我的手去拿一杯水），此时我的手臂各个关节应该运动到哪个关节位置呢？这个问题显然是机器人学需要研究的一个根本问题——因为对于任意机械臂，你想控制的量在操作空间，而你能控制的量却在关节空间。想要控制end effector在操作空间完成特定操作，就一定避不开逆运动学这个问题。

逆运动学最基本的思路，是从正运动学反过来，比如以我们最熟悉的RR平面机械臂为例

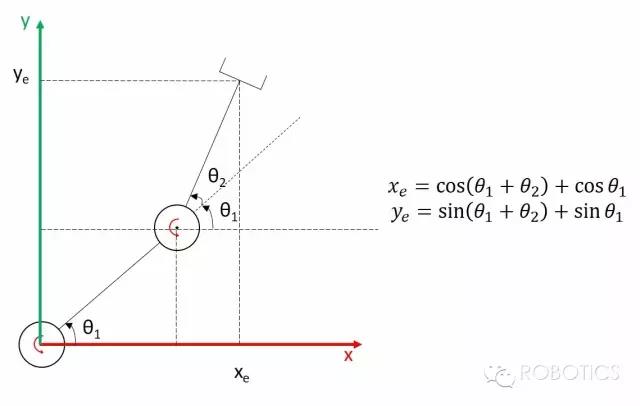
它的逆运动学问题是：已知操作空间$(x_e,y_e)$，怎么求关节空间$(\theta_1,\theta_2)$？

很明显我们有两个未知数、两个方程，解解方程就行了。当然，这明显是一个非线性方程组，怎么解？我是把两个等式都两边平方然后相加，可以求出$\theta_2$，然后再求出$\theta_1$。

如果是一个六自由度的机械臂，我们用包含关节位置的Transformation Matrix（齐次坐标变换矩阵）来表示end effector的位置和朝向，这个矩阵包含了end effector position w.r.t {0}（一个3×1的向量），以及end effector的旋转矩阵w.r.t {0}（一个3×3的矩阵），一共12个未知数，这时候逆运动学又怎么求呢？

如果是一个七自由度的机械臂，我们说这时候机械臂存在冗余自由度，end effector固定不动的时候关节仍然可以运动，这时候逆运动学又怎么求呢？

由于逆运动学非线性、解不一定存在或不是唯一等特性，比起正运动学直截了当的写矩阵，求解逆运动学就要困难得多，也因此有很多不同的方法：

  • 解析法（Analysis Solution），顾名思义是用代数或几何大法直接求解，如上面的例子所示。通常随着自由度上升，求得解析解的难度也越来越大，对于冗余机械臂还需要从几个解中选择合适的解。这种方法通常用在特定几何结构的机械臂，并且有特定的关节位置求解顺序。这里有一个视频，展示了一个六自由度KUKA KR 60机械臂的解析解求解方法，视频链接。由于解析解法不具有通用性，我们后面不再详述。

  • 优化法（Optimization-based Solution），是把问题转化为一个优化问题求数值解。用数学语言表达，就是把求 $$ q = f^{-1}(x) $$

    的问题，转化为"求关节位置q，使实际end effector位置x与正运动学算出的end effector位置发f(q)之间的差值最小"的问题： $$ \min_q,where \ e = {(x - f(q))}^2 $$ 如何求解上面这个式子（比如用梯度下降大法Gradient Descent）就是一个数学问题了，所以本文也不再详述。

  • 迭代解 - 雅可比矩阵求逆法（Iterative Method - Jacobian Inverse），是把问题“微分化”，利用瞬时运动学的逆运算无限逼近 $$ \dot{x} = J \dot{q} \Rightarrow \dot{q} = J^{-1} \dot{x} $$

  • 雅可比矩阵转置法（Jacobian Transpose），是从下面式子出发，用雅可比矩阵的转置代替困难的求逆运算 $$ \tau = J^TF $$ 由于在逆运动学求解中，我们不关心系统的动力学特性，上面这个式子也可以写成 $$ \dot{q} = J^T \dot{x} $$

上面这两个方法相对比较通用（是否工业上常用？这个很难说。可能工业上对特定机械臂用解析解的也不少……），所以这篇文章主要还是给我们的老朋友雅可比矩阵解锁新功能，本文将着重介绍雅可比矩阵求逆法。

2 迭代解-雅可比矩阵求逆（Jacobian Inverse）

雅可比矩阵求逆的方法有什么优点呢？我们还是拿那个两自由度机械臂举例：

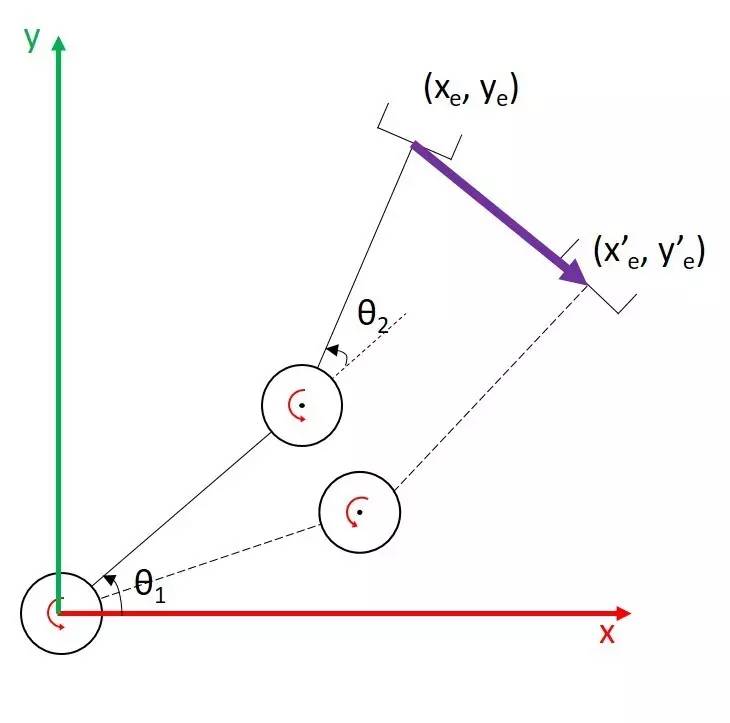
假设link的长度都是1，那我们可以求出它的解析解为： $$ \theta_2 = {\cos}^{-1} \frac{x^2 + y^2 - 2}{2} \\
\theta_1 = \frac{-x \sin\theta_2 + y \cos\theta_2 + y}{y \sin\theta_2 + x \cos\theta_2 +x} $$ 现在我们需要end effector从图中$(x_e,y_e)$沿紫色直线运动到$(x'_e,y'_e)$，但需要控制关节位置实现这一点。现在有以下思路——

Ⅰ.求起点和终点对应的关节位置，直接对这两处关节位置进行线性插值求得关节运动轨迹——这样虽然省了很多计算量，但end effector不大可能沿着直线走；

Ⅱ.把这条直线插入很多很多中间点，每一个点都求出对应的关节位置，然后控制每一个关节按着这一系列的关节位置走（就是我们前面说的解析/优化解法）；

Ⅲ.还是把这条直线插入很多很多中间点，但如果点与点的间隔足够小、运动时间足够短，我们就可以在每一点用雅可比矩阵求逆来求得当前关节位置的变化——换个角度讲，我们也可以设定end effector沿这条直线的运动速度，用雅可比矩阵求逆求得关节速度，直接控制关节的运动速度而不是位置。

我们将第三个方法画成控制框图：

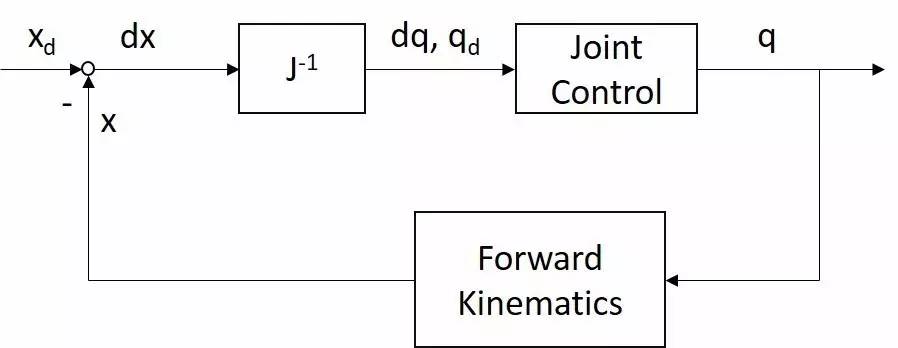
图中$x_d$的下标d表示“desired”，即你希望x到达的位置和朝向；以后还有下标c表示“current”，即当前x的位置/朝向；我们会经常看到这样的下标。

你可能不懂控制框图，没关系，首先上面一行Joint control（关节控制）之前，从左到右说的是： $$ dx = x_d - x \\
dq = J^{-1}dx \\
q_d = dq + q_c $$ Joint control则是你把你计算出来的$q_d$送到每一个关节的控制器中（比如最简单的舵机）；这些控制器最终把各个关节控制到位置q（好的控制器，大部分情况q和$q_d$应当非常接近）

这个图的下边一行说的是，我们又从这个关节位置q用正运动学求出了此时的end effector位置x，反馈到前面再给上面第一个式子运算求dx。

通常你设置一个$x_d$，控制器需要走几遍这个控制回路才能将dx降到接近0（让x逼近$x_d$），因此这个方法也被称为迭代法。

3 冗余雅可比矩阵求逆

你一定想问，当雅可比矩阵不可求逆的时候怎么办呢？不可求逆的情况有很多种，我们这里先讨论一种：即当雅可比矩阵是矮胖型，机械臂具有冗余自由度的情况。

这个时候要用到一个数学概念，叫伪逆矩阵（pseudoinverse）。伪逆矩阵也有很多种，在机器人逆运动学中用得较多的是右伪逆矩阵（right-inverse）。如果把伪逆矩阵记为A+，left-inverse是说(A+)A = I；而right-inverse就是说A(A+) = I。

Right-inverse是通过求解下面这个问题得到的： $$ \min_{\dot{q}} {\Vert{\dot{q}} \Vert}^2 \\
subject \ to \ \dot{x} = J\dot{q} $$ 在机器人中，我们会希望每一次迭代的关节运动量尽可能小（从多种可能的运动方式中选出运动最少的一种），所以上面说的是**求一个尽可能小的能满足方程的dq**

用拉格朗日乘数法（Lagrange Multiplier）,这个问题可以变成： $$ \min_{\dot{q}} \frac{1}{2}{\Vert{\dot{q}} \Vert}^2 + \lambda^T(\dot{x} - J\dot{q}) $$ （乘1/2是为了后面求导后不要有个讨厌的2——不影响结果）

拉格朗日乘数法是一个求约束条件下极值的方法，非常有用，用起来也比较简单，而且我们以后还会用到——如果你不是很了解，我强烈建议你去自学一下。

要求极值，必先求导——拉格朗日乘数法是分别对dq和$\lambda$求导，导数为0时可求得极值（我们就不论证这里是极小值了）： $$ \frac{d\frac{1}{2}{\Vert{\dot{q}} \Vert}^2 + \lambda^T(\dot{x} - J\dot{q})}{d\dot{q}} = \dot{q}^T - \lambda^TJ = 0 \\
\frac{d\frac{1}{2}{\Vert{\dot{q}} \Vert}^2 + \lambda^T(\dot{x} - J\dot{q})}{d\lambda} = \dot{x} - J\dot{q} = 0 $$ 解上面两个方程，即可求出 $$ \dot{q} = J^T \lambda \\
\dot{x} = J\dot{q} = JJ^T\lambda \stackrel{solve \ \lambda}{\Longrightarrow} \ \lambda = (JJ^T)^{-1} \dot{x} \\
\dot{q} = J^T(JJ^T)^{-1}\dot{x} \\
\therefore J^{+} = J^T(JJ^T)^{-1} $$ 不难验证$JJ^+=I$。用这个$J^+$求解出的dq即为满足条件的最小关节运动速度。最后简单地提一下null space，我们可以验证： $$ \forall \dot{q},J(I-J^{+}J)\dot{q}_0 = 0 $$ 这说明矩阵$I-J^+J$可以把任意关节速度投影到“零空间”内，投影后的关节速度将不引起任何end effector的运动。利用这个特性，我们可以在满足了end effector的$x_d$之后，再利用零空间实现其它任务（比如避开障碍物）。

为了不一下子扔太多东西，这篇文章就到此为止吧。下一篇文章我们会讲雅可比矩阵求逆法存在的问题和解决方法、雅可比矩阵转置法、再酌情提一些其它的逆运动学求解算法。说起来，逆运动学这个问题真是麻烦得不行，解法也是五花八门呢……