0 回顾
这是关于雅可比矩阵的第三篇文章。我们回顾下前面的内容,雅可比矩阵从何而来、如何求之。
首先我们在学习正运动学——即如何将关节空间的位置映射到操作空间的位置及朝向这个问题之后,第二个问题就是瞬时运动学——如何将关节空间的速度映射到操作空间的速度。经过推导,我们发现,雅可比矩阵就是解出这个映射的关键:
$$
\dot{x} = J \dot{q}
$$
其中,
$$
J = \begin{bmatrix}
\frac{dx_1}{dq_1} & \dots & \frac{dx_1}{dq_n} \\
\vdots & \ddots & \vdots \\
\frac{dx_m}{dq_1} & \dots & \frac{dx_m}{dq_n}
\end{bmatrix}
$$
雅可比矩阵有m行n列:m为操作空间的自由度,n为关节空间的自由度(或说关节数量)。
基本雅可比矩阵(Basic Jacobian)是由笛卡尔坐标描述操作空间线速度及角速度求得,可分为两部分:线速度雅可比矩阵$J_v$和角速度雅可比矩阵$J_w$,分别求解。
$$
J = \begin{bmatrix}
J_v \\
J_w
\end{bmatrix}
$$
求解基本雅可比矩阵需要先求解正运动学。一个链式机械臂的$J_v$由end effector的位置对关节位置求导得到;$J_v$由每一个旋转关节的旋转轴单位向量得到——具体求解方法请复习上一篇。理解这个简单的求解方法对理解雅可比矩阵大有益处!
回顾完毕,现在我们可以来和雅可比矩阵进行一场更深入的交流……
1 力传递(Force relationship)
在研究了关节空间与操作空间的位置映射关系和速度关系以后,我们继续思考:那么它们的力/扭矩映射关系又如何?举例说明——如果别人抓着你的手用力想把它从你戳红包的屏幕上移开,你的肩膀、手肘、手腕等各处关节(这里假设身体的其他部分没有作用且固定了)各自需要输出多大的力矩才能让你的手保持不动呢?如果你要锤击一个沙包,它们又需要输出多大的扭矩呢?
很神奇的是,雅可比矩阵同样也是连接关节空间与操作空间力/扭矩映射关系的纽带。
现在我们设在关节空间,关节输出的力/扭矩为: $$ \tau = {[\tau_1 \quad \tau_2 \quad \dots \quad \tau_n]}^T $$ 关节运动速度为 $$ \dot{q} = {[\dot{q}_1 \quad \dot{q}_2 \quad \dots \quad \dot{q}_n]}^T $$ 注意我们使用的始终是列向量(这是在第二篇文章中就约好了的^o^)。
那么整个系统输出的功率(等于力乘速度)在关节空间即表示为 $$ P = {\tau}^T \dot{q} $$ 希望你一眼就明白这是个向量点乘,P显然是一个标量……
现在从操作空间的角度看,设此时end effector能够对外界输出的力/扭矩(或说为了维持整个系统的静态平衡,外界对end effector的作用力/扭矩)为 $$ F = {[f_1 \quad f_2 \quad f_3 \quad n_1 \quad n_2 \quad n_3]}^T $$ 其中f表示力,n表示扭矩。
end effector的速度则为
$$
\dot{x} = {[\dot{x}_1 \quad \dot{x}_2 \quad \dots \quad \dot{x}_n]}^T
$$
那么施加在end effector上的外力对整个系统做功的功率即为
$$
P = F^T \dot{x}
$$
由能量守恒定律,我们必须有
$$
P = {\tau}^T \dot{q} = F^T \dot{x}
$$
带入瞬时运动学的式子:
$$
{\tau}^T \dot{q} = F^T \dot{x} \\
\tau^T = F^TJ = (J^TF)^T \\
\tau = J^TF
$$
注:$(AB)^T = B^TA^T$
经过漫长的推导,我们得到雅可比矩阵的另一个重要用途:J的转置乘以操作空间的力/扭矩就可得到关节空间输出的力/扭矩!这是一个从操作空间到关节空间的映射,与我们之前讲到的正运动学、瞬时运动学方向正好相反。
应该庆幸,当别人试图把你的手掰到别处时,你的大脑已经把测量你的手受到的外力(F)、计算你手臂的雅可比矩阵的转置、求出每个关节需要输出的力并执行这整个过程,在你完全不知道的情况下完成了。
那么对于真正的机械臂而言,学习这个力映射关系又有什么意义呢?对于最传统的位置控制机器人,依赖对位置精确的传感,基于一种不达目的地绝不罢休的精神运动,这个式子可能确实没什么用。但是,越来越多的应用场景要求机器人能够在某一位置/某一方向维持特定的力(比如抓握一个物体、擦玻璃)、或者在一个复杂环境中安全工作(保证不会在碰到障碍物时对物体施加过大的作用力);要实现这样的控制,这个映射关系必不可少——我们以后会更详细地讲解这个式子的应用。
2 奇异(Singularity)
我们在《从RP入门机器人学》中提到了Singularity这个问题,简单地说,Singularity就是机械臂处在某一个configuration(即特定的关节位置组合)时,end effector失去某个方向的自由度——你手臂伸直的那一刻,你的手绝无法沿着你手臂的方向运动。
现在有了雅可比矩阵,我们可以从数学的角度重新来认识Singularity。为什么呢?不要忘了雅可比矩阵的用处:关节的运动速度乘以雅可比矩阵即得到end effector的运动速度。而end effector失去某个方向的自由度即意味着在机械臂到达那个configuration的瞬间,不管关节怎么运动,end effector在这个方向的速度总为0。
从线性代数的角度来说,此时的J矩阵有这样的特性:对所有任意向量a,$J_a$相乘得到向量b,则所有向量b组成的线性空间维度将比正常情况下少至少一个自由度——这说明什么?说明这个时候的雅可比矩阵遭遇了降维攻击,被降秩了啊!
我们以RR平面机械臂举例:
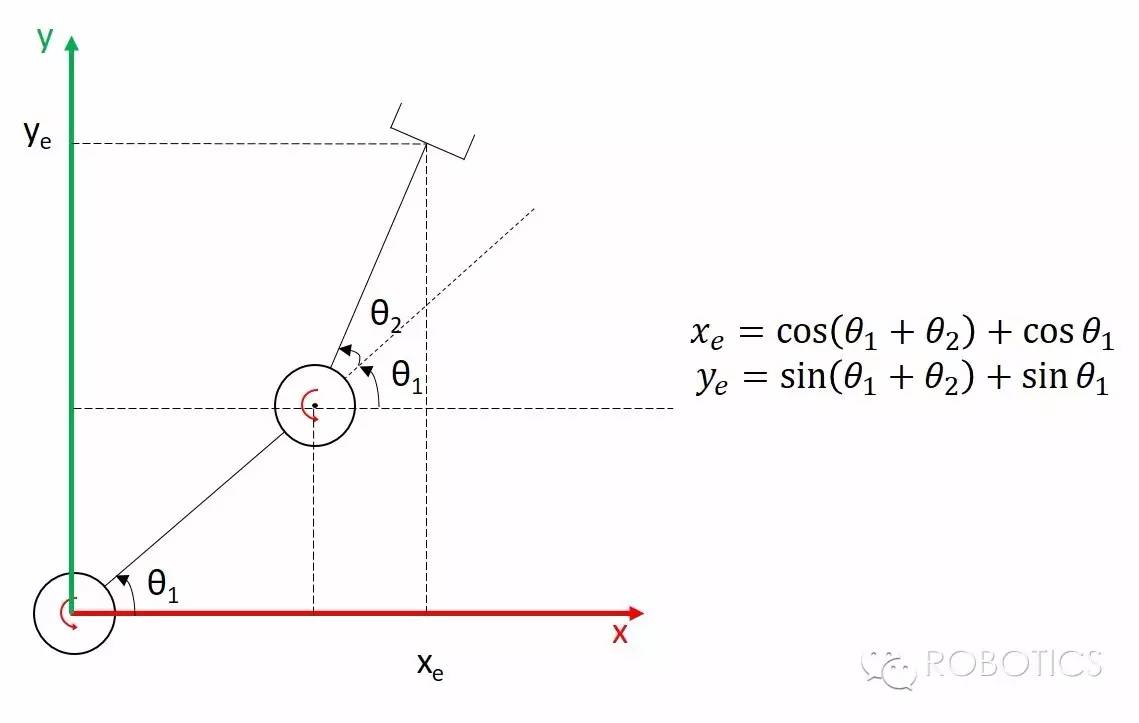
这个机械臂的雅可比矩阵为:
$$
J = \begin{bmatrix}
\frac{dx_e}{d\theta_1} & \frac{dx_e}{d\theta_2} \\
\frac{dy_e}{d\theta_1} & \frac{dy_e}{d\theta_2}
\end{bmatrix}
= \begin{bmatrix}
-\sin(\theta_1 + \theta_2) - \sin\theta_1 & -\sin(\theta_1 + \theta_2) \\
\cos(\theta_1 + \theta_2) + \cos\theta_1 & \cos(\theta_1 + \theta_2)
\end{bmatrix}
$$
现在,为了求出在什么configuration下机械臂会遇到奇异点,即求这个雅可比矩阵什么时候不是满秩矩阵,我们可以直接利用此时J的特征值为0(即此时J是一个奇异矩阵)求得:
$$
det(J) = -\cos(\theta_1 + \theta_2) (\sin(\theta_1 + \theta_2)+\sin\theta_1) + \sin(\theta_1 + \theta_2)(\cos(\theta_1 + \theta_2)+\cos\theta_1) = 0
$$
稍微计算一下(三角恒等式什么的也是要很熟的!)可得:
$$
\sin(\theta_1 + \theta_2)\cos\theta_1 - \cos(\theta_1 + \theta_2)\sin\theta_1 = 0 \\
\sin(\theta_1 + \theta_2 - \theta_1) = \sin\theta_2 = 0
$$
所以singular configuration是$\theta_2=0$!此时,机械臂“伸直”,end effector无法在沿机械臂link的方向上运动。将这个值代入原矩阵,会发现J的行/列向量不是线性独立,它的秩为1。
在数学上,奇异矩阵的说法只对方阵有效,求特征值也是只对方阵有效。对于机器人来说,(Kinematic)Singularity是机器人在某一个configuration时end effector运动空间的降维,与雅可比矩阵的形状并无关——只是当雅可比矩阵不是方阵时,我们需要先把冗余自由度去掉再求解。
3 冗余(Redundancy)
说到冗余自由度,相信你已经可以想到如何从雅可比矩阵看出冗余了——当它又矮又胖的时候就是啦。在第一篇文章中也曾用你的手举例,因为人的手在关节空间有七个自由度,所以你能够在手部固定的情况下移动你的手肘。从数学的角度上,这意味着 $$ \exists \dot{q},J\dot{q} = 0 $$ 不得不感叹数学语言真的是简洁优美……
我们知道,假如A是一个方阵,那么Ax=0有非零解的充分必要条件是A是一个奇异矩阵——也就是说,如果没有冗余自由度,一个机械臂关节运动而end effector不动的情况只有在它处于singularity时才能出现。但是,如果A是一个矮胖矩阵,那么Ax=0必然有无数个非零解,这些解组成的空间即称为“零空间”(nullspace)。
简单地提一下:对于一个有冗余自由度的机器人,假设你除了要控制end effector运动到某一位置,还要保证过程中它的手肘不碰到障碍物,那你总是可以在nullspace中找到一组解满足你的要求:在不改变end effector轨迹的同时避开障碍物。这样的方法称为null space control,我们以后有机会会详细展开。
希望今天这篇文章能让你对雅可比矩阵在机器人学中的重要地位有更强烈的认识,对这个系列一开始提到的机器人的奇异、冗余等问题有更深刻的理解。当然了,希望至少也帮你复习了一下线性代数吧。
三篇关于雅可比矩阵的文章终于写完了,但是它仍然会不停地出现在以后的文章中——逆运动学、动力学、机器人控制,哪里都有它的影子。在我看来,它是连接机械、物理与数学的桥梁,优美得无与伦比呢。