上一篇文章我们从正运动学公式推导出瞬时运动学公式,推出著名的雅可比矩阵,并例举出了一个特别简单的例子以提供直观印象。简单回顾一下——
瞬时运动学解决了如何从关节速度得到end effector速度问题: $$ \dot x = J \dot q $$ 其中,J表示雅可比矩阵(Jacobian Matrix): $$ J = \begin{bmatrix} \frac{dx_1}{dq_1} & \dots & \frac{dx_1}{dq_n} \\
\vdots & \ddots & \vdots \\ \frac{dx_m}{dq_1} & \dots & \frac{dx_m}{dq_n} \end{bmatrix} $$ 雅可比矩阵的物理意义,以第5行第3列举例来说,表示当第3个关节转动/平移足够小的一定量(微分概念)时,乘上这个值就等于end effector在第5个自由度上相应的转到/平移量。
1 基本雅可比矩阵(Basic Jacobian)
1.1 定义
上面说end effector第5个自由度,到底指的是哪个自由度?显然,这取决于我们如何描述end effector的运动。举个例子来说,假如我们有一个全自由度的end effector (即3个转动DOF,3个平动DOF),那我们可以定义前3个自由度为沿某个坐标系(一般指世界/基坐标系)的x,y,z轴平移,后三个自由度为绕该坐标系的x,y,z轴旋转——这样我们说的第5个自由度,指的是绕这个坐标系的y轴旋转。实际雅可比矩阵的结果,完全取决于我们选取的坐标系与描述end effector运动的顺序。
所以,我们把用笛卡尔坐标系描述线速度(linear velocity)和角速度(angular velocity)、以机械臂的基坐标系(Base frame)或frame {0}作为参考系来描述end effector速度所求的雅可比矩阵,称为基本雅可比矩阵;其他所有表示方法(如将笛卡尔坐标系改为柱坐标系、球坐标系;角度改为欧拉角、四元数quaternion等)都可以由这个基本雅可比矩阵转换得到。根据上面基本雅可比矩阵的定义,end effector的速度可以写为:
$$
\dot x = \begin{bmatrix}
v_x \\
v_y \\
v_z \\
w_x \\
w_y \\
w_z
\end{bmatrix}
= \begin{bmatrix}
\vec v \\
\vec w
\end{bmatrix}
$$
相应的,雅可比矩阵也可以写成:
$$
J = \begin{bmatrix}
J_v \\
J_w
\end{bmatrix}
$$
从J的表达式中很容易可以看出,上半部分对应线速度、下半部分对应角速度。
1.2 线速度部分
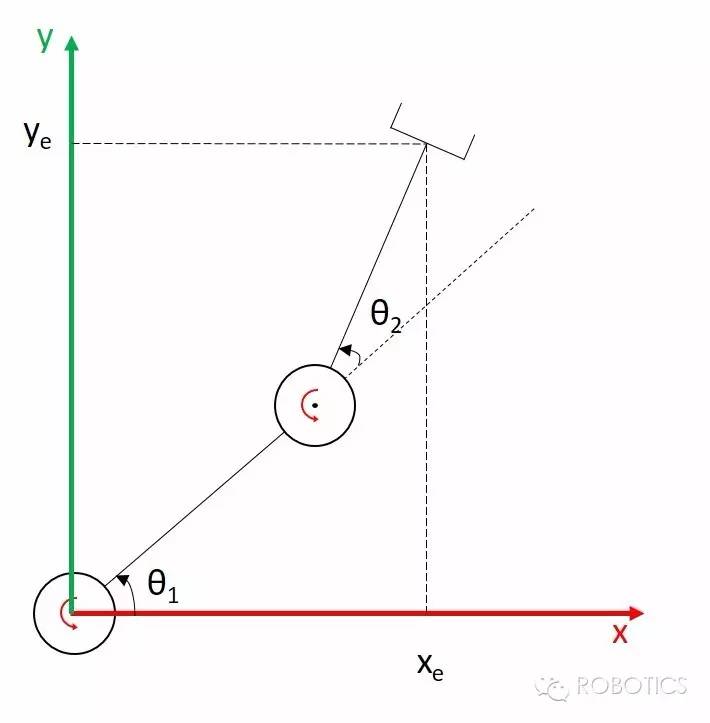
首先从我们比较容易理解的上半部分$J_v$开始,以之前讲的RR机械臂为例,我们是怎么求出雅可比矩阵的?
- 先写出end effector位置的正运动学表达式
$$
x_e = \cos{(\theta_1 + \theta_2)} + \cos{\theta_1} \\
y_e = \sin{(\theta_1 + \theta_2)} + \sin{\theta_1}
$$
- 再用操作空间的位置向量对关节空间的位置向量求导
$$
J = \begin{bmatrix}
\frac{dx_e}{d\theta_1} & \frac{dx_e}{d\theta_2} \\
\frac{dy_e}{d\theta_1} & \frac{dy_e}{d\theta_2}
\end{bmatrix}
= \begin{bmatrix}
-\sin(\theta_1 + \theta_2) - \sin\theta_1 & -\sin(\theta_1 + \theta_2) \\
\cos(\theta_1 + \theta_2) + \cos\theta_1 & \cos(\theta_1 + \theta_2)
\end{bmatrix}
$$
根据瞬时运动学的定义,这个方法是非常直观的。那如果我们的机械臂复杂一点,需要用到齐次坐标变换来求正运动学公式呢?
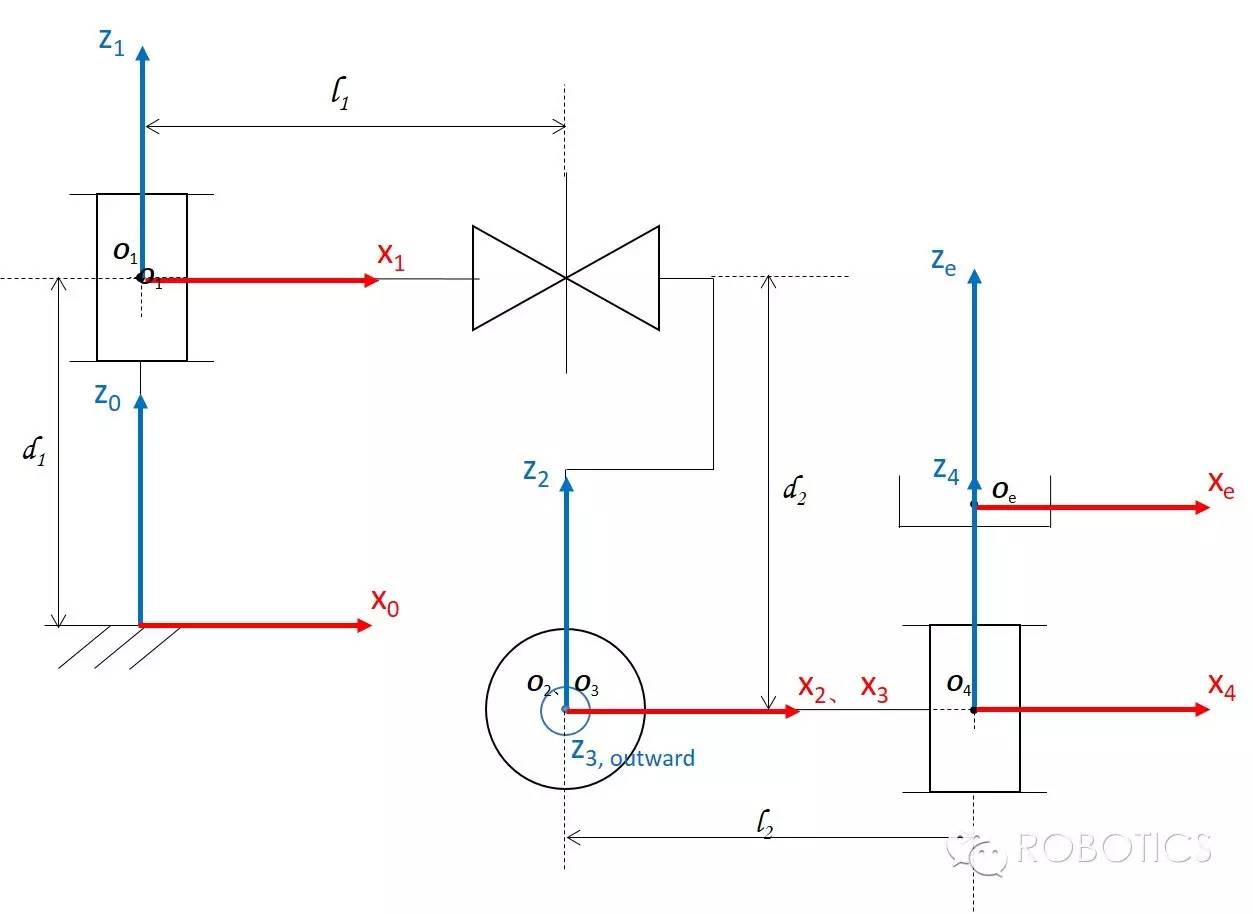
这是我们求出来end effector的正运动学表达式(查看《“正运动学”——从关节空间到操作空间》),这里假设图中$O_e$和$O_4$是重合的:
$$
{}^0_eT = \begin{bmatrix}
× & × & × & l_2c\theta_1c\theta_3 + l_1c\theta_1 \\
× & × & × & l_2s\theta_1c\theta_3 + l_1s\theta_1 \\
× & × & × & l_2s\theta_3 + d_2 \\
0 & 0 & 0 & 1
\end{bmatrix}
$$
由于这里不要旋转矩阵,只需要平移矩阵,我们又假设$O_e$和$O_4$是重合的,则平移矩阵表达的是end effector的位置w.r.t frame{0}。
所以,我们要求的$J_v$,只需要对平移矩阵对关节空间向量($v_1,d_2,v_3,v_4$)求导即可,按照向量求导的规则,我们得到是一个3 x 4的矩阵:
$$
J_v = \begin{bmatrix}
-l_2s\theta_1c\theta_3 - l_1s\theta_1 & 0 & -l_2c\theta_1s\theta_3 & 0 \\
l_2c\theta_1c\theta_3 + l_1c\theta_1 & 0 & -l_2s\theta_1s\theta_3 & 0 \\
0 & 1 & l_2c\theta_3 &0
\end{bmatrix}
$$
1.2 角速度部分
说完$J_v$,我们要来说下半部分的$J_w$了。这个矩阵其实很容易求,但是要理解它则需要一点小“技巧”。我们还是先从最简单的平面机械臂看起:
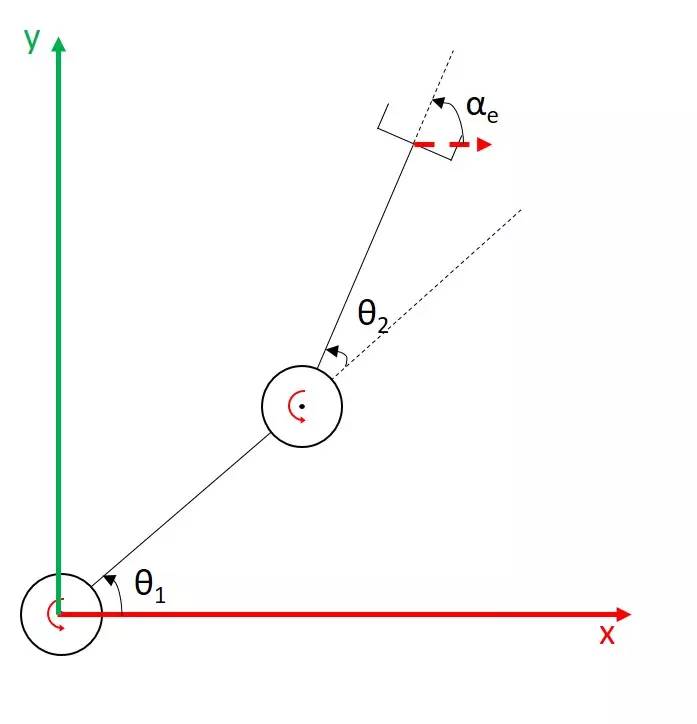
这次,我们只关心end effector的朝向。对于平面机械臂而言,end effector只有一个转动自由度,即图中标出的α(设与x轴重合时为0°,从x轴旋转到y轴为正方向)。此时我们的操作空间为(α),关节空间还是($\theta_1,\theta_2$);根据定义,我们求解的雅可比矩阵角速度部分如下: $$ J_{w} = \begin{bmatrix} \frac{d\alpha}{d\theta_1} & \frac{d\alpha}{d\theta_2} \end{bmatrix} $$ 对于这个平面机械臂而言,我们很容易可以看出:$\theta_1$转多少度,$\alpha$就转动多少度;同理$\theta_2$也是。则$J_w$应为[1, 1]。
举这个例子,希望它能帮助我们建立一个直观印象和基本概念——一个机械臂的旋转关节绕某个轴转多少角度,他的end effector就会相应地绕这个轴多少角度;在平面机械臂的情况中,这表示一个旋转关节的转速乘以1即可得到它引起(Contribute)的end effector转动的速度,因此上面的$J_w$为[1,1]。
在三维空间里,角速度定义为一个指向旋转轴的向量,其方向可以由右手定则确定。因为我们定义机械臂的每个旋转关节都是绕自身的Z轴旋转的,所以当每一个旋转关节转速为$w$时,它所contribute的end effector的角速度向量以这个旋转关节本身的坐标系为参照系必然为$[0,0,w]$。换句话说,这个旋转关节的转速乘以[0,0,1]可以得到它所引起的end effector的角速度(w.r.t 该旋转关节坐标系)。(end effector的实际速度可由不同旋转关节contribute的角速度线性叠加。)
由于我们基本的雅可比矩阵是以frame{0}为参考系的,为了写出$J_w$,我们需要把每个旋转关节的z轴[0,0,1],从以关节自身坐标系为参考系转换到基准坐标系frame{0}表示。另外,对于平移关节,因为平移关节的运动不可能改变end effector的朝向,故end effector的orientation对平移关节位置的求导一定是0!
以前面出现的RPRR机械臂为例,它的雅可比矩阵角速度部分是这样的: $$ J_w = \begin{bmatrix} {}^0\hat{Z}_1 & \vec{0} & {}^0\hat{Z}_3 & {}^0\hat{Z}_4 \end{bmatrix} $$ 看明白了么?
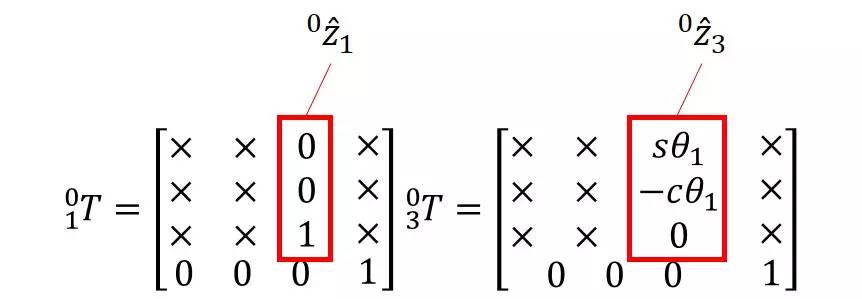
现在我们只剩最后一个问题就是怎么把各个关节的z轴坐标w.r.t frame{0}求出来——其实算一遍各个关节的齐次坐标变换矩阵。例如${}^0_1T,{}^0_3T$:
1.3 小结
-
基本雅可比矩阵的上部分$J_v$由end effector的位置向量对关节求导得出;
-
end effector的位置向量可由正运动学得到
-
基本雅可比矩阵的下半部分$J_w$可由每个旋转关节的z轴以基准坐标系为参考系写出的单位向量得到
-
把$J_v$和$J_w$合起来可以得到一个m × n的矩阵,其中m是end effector/操作空间的自由度(对于空间机械臂通常m=6),n是机械臂的关节数量。
2 其它雅可比矩阵
最后简单地提一下,得到Basic Jacobian 后,要求其他形式的雅可比 矩阵都不是问题,只需要乘一个转换矩阵就可以了。比如说,如果你的end effector位置是由柱坐标表示的,即$(\rho,\theta,z)$,而坐标转换为笛卡尔坐标是:
$$
x = \rho \ \cos{\theta} \\
y = \rho \ \sin{\theta} \\
z = z
$$
那么转换矩阵E~p~(这里的p表示position)就由笛卡尔坐标对柱坐标的向量求导得出:
$$
E_p = \frac
{d\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
}
{d\begin{bmatrix}
\rho \\
\theta \\
z
\end{bmatrix}
}
= \begin{bmatrix}
\cos{\theta} & \sin{\theta} & 0 \\
-\rho\sin{\theta} & \rho\cos{\theta} & 0 \\
0 & 0 & 1
\end{bmatrix}
$$
而新的雅可比矩阵的上半部分就等于基本雅可比矩阵的$J_v$左乘上这个$E_p$。对于旋转也类似——大家了解一下就好,不再详细展开了。
这篇文章主要讲了Basic Jacobian的求法,新的内容不多,但希望能够让你对雅可比矩阵有更进一步了解。上次说要讲雅可比矩阵与Singularity、Redundancy的关系,还说要解矮胖的线性方程……篇幅所限,只能留到下一篇了。毕竟雅可比矩阵这么重要,为它多写一篇也不为过呢!