看懂本文,除了了解矩阵、向量、向量点乘、矩阵向量相乘等内容,以及看明白我们该系列的前四篇文章外,你还需要懂得简单的向量求导运算——其实很简单啦,如果你不知道怎么对向量求导,那就把它当一列标量一个一个写出来,比如这样: $$ \frac{d\vec{x}}{d\vec{q}} = \frac { d{\begin{bmatrix} x_1 \\
x_2 \\ x_3 \end{bmatrix} } } { d{\begin{bmatrix} q_1 \\
q_2 \end{bmatrix} } } = \begin{bmatrix} \frac{dx_1}{dq_1} & \frac{dx_1}{dq_2} \\
\frac{dx_2}{dq_1} & \frac{dx_2}{dq_2} \\
\frac{dx_3}{dq_1} & \frac{dx_3}{dq_2} \end{bmatrix} $$不知道行列怎么分布?把分母乘到右边,算一下左边是3×1向量,右边是3×2矩阵乘以2×1向量 = 3×1向量,左右相等,搞定!简单粗暴,方便有效。哎呀,一不小心,把雅可比矩阵(Jacobian Matrix)都给写出来了呢。(想要知道数学上是怎么定义推导出向量求导方法的请去上数学课,我只负责教你记住啦😄)
上一篇文章我们利用DH参数与坐标变换,推到了机械臂的“正运动学”求解方法:只要知道机械臂的结构以及每个关节的位置(关节位置,指的是旋转关节的角度以及平移关节的平移),就可以求出end effector的位置和朝向,即完整的end effector的齐次变换矩阵w.r.t基座/地面坐标系。“正运动学”通常对应“逆运动学”,这篇文章先聚焦“瞬时运动学”;因为它与前面的内容一脉相承,在一类机器人控制的理论框架中,也比逆运动学更重要。
瞬时运动学(Instantaneous kinematic)也是描述从关节空间到操作空间的映射,“瞬时”表明它不是描述“静态”的文章,而是描述“动态”的速度。还记得正运动学要求解的“函数“是什么吗?如下所示: $$ \vec{x}=f(\vec{q}) $$ 其中,q向量表示关节位置,x向量表示end effector的位置和朝向。
在上一篇文章的正运动学求解中,由于空间朝向表示的复杂性,我们最终用齐次坐标变换矩阵T来表示end effector的位置和朝向,而不是一个向量。不过,从数学的角度或抽象理解的角度来讲,上面的式子显然更为通用(更何况我们有“一百种”办法可以用向量来表示空间朝向,分分钟抛弃旋转矩阵)。
现在,当我们说“瞬时运动学”求解的是从关节空间到操作空间的速度映射时,由于速度描述的是短时间内的位置变化,即位置对时间的导数,相信你很自然地会想到我们需要求解这样一个函数:
$$
\frac{d\vec{x}}{dt} = g(\frac{d\vec{q}}{dt}) \\
or \\
\dot{x} = g(\dot{q})
$$
现在我们的任务就是,从“正运动学”公式推导出“瞬时运动学”公式:
$$
\frac{d\vec{x}}{dt} = \frac {df(\vec{q})}{dt}
= \frac {df(\vec{q})}{d\vec{q}} \cdot \frac {d\vec{q}}{dt} \\
i.e: \ \dot{x} =\frac{d\vec{x}}{dq} \cdot \dot{q}
$$
有没有觉得上面的式子某个地方很眼熟啊?没错,就是我们一开始提到的向量x对向量q的求导了!将关节空间的速度与操作空间的速度连接起来的,就是由向量求导获得的雅可比矩阵。现在,让我们把这个重要的结论用数学方式表示出来,用J表示向量x对向量q的导数:
$$
\dot{x} = J\dot{q}
$$
根据一开始讲的向量求导方法,J是一个矩阵。这个矩阵其实一点也不抽象:如果我们仔细看它的每一个元素,就会发现它的第i行第j列表示的物理意义就是当第j个关节运动时,操作空间的第i个平动/转动方向会如何运动:
$$
J = \begin{bmatrix}
\frac{dx_1}{dq_1} & \cdots & \frac{dx_1}{dq_n} \\
\vdots & \ddots & \vdots \\
\frac{dx_m}{dq_1} & \cdots & \frac{dx_m}{dq_n}
\end{bmatrix}
$$
比如第一行第一列,就表示当第一个关节运动某个角度/距离时,end effector相应的在x1这个方向上运动/转动某个距离/角度。如果你还是觉得太抽象,那我们来看一个例子,还是上一篇文章用到的那个平面机械臂:
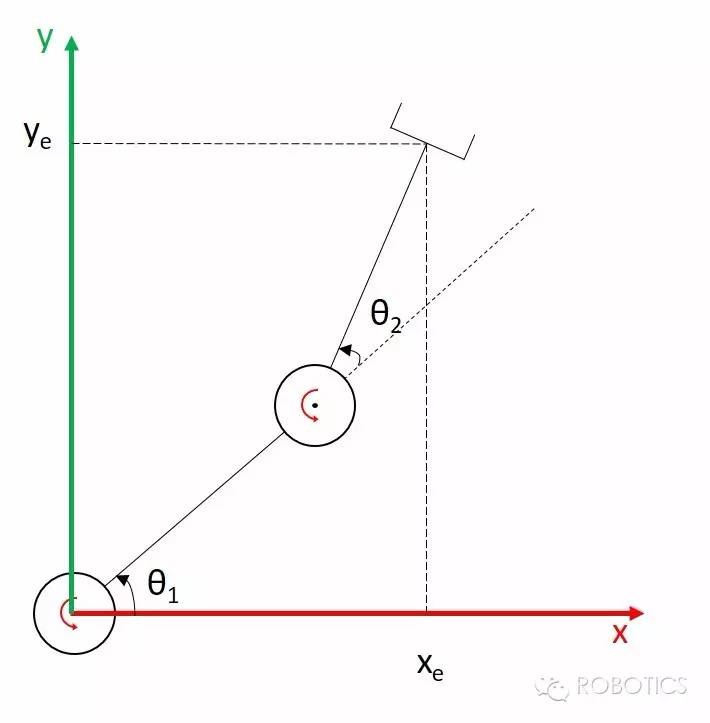
我们的关节空间是$(\theta_1,\theta_2)$,操作空间是$(x_e,y_e)$,我们也写出了正运动学公式(将link的长度都定为1):
$$
x_e = \cos(\theta_1 + \theta_2) + \cos\theta_1 \\
y_e = \sin(\theta_1 + \theta_2) + \sin\theta_1
$$
那么雅可比矩阵就是:
$$
J = \begin{bmatrix}
\frac{dx_e}{d\theta_1} & \frac{dx_e}{d\theta_2} \\
\frac{dy_e}{d\theta_1} & \frac{dy_e}{d\theta_2}
\end{bmatrix}
= \begin{bmatrix}
-\sin(\theta_1 + \theta_2) - \sin\theta_1 & -\sin(\theta_1 + \theta_2) \\
\cos(\theta_1 + \theta_2) + \cos\theta_1 & \cos(\theta_1 + \theta_2)
\end{bmatrix}
$$
注意在我们这个例子中,关节空间有两个自由度、操作空间也有两个自由度,所以我们的雅可比矩阵是正方形的(square matrix);但雅可比矩阵不一定是方阵,这一点大家要记住。
如果你考虑一下当$\theta_1$为0, $\theta_2$为90°的时候,代入算一下,我们会得到这样的雅可比矩阵:
$$
J = \begin{bmatrix}
-1 & -1 \\
1 & 0
\end{bmatrix}
$$
对应的机械臂:
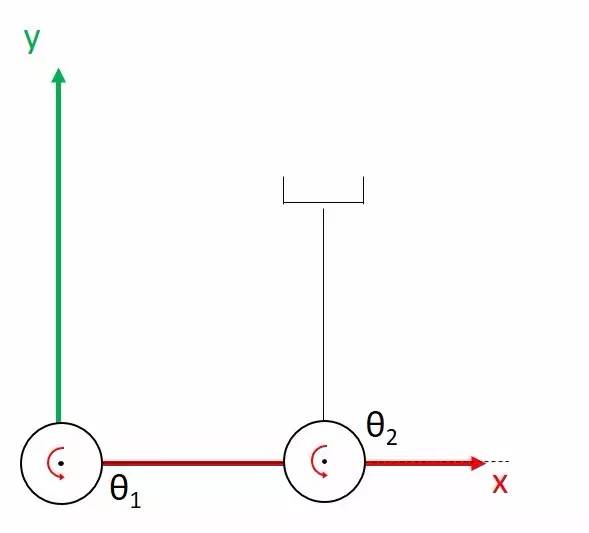
现在你看,如果我们保持第一个关节不动、转动第二个关节,那么在这一个瞬间end effector将只能在x方向运动,速度为1(线速度等于角速度乘以半径,即link的长度),y方向的速度则为0,所以J矩阵的第二列是[-1, 0]。
而如果我们保持第二个关节不动、转动第一个关节,end effector的瞬时速度将与end effector与第一个关节轴的连线垂直,其半径为√2,则线速度为√2,分解为x方向的-1和y方向的1,所以J矩阵的第一列为[-1, 1]。
希望这么啰嗦的解释可以让你获得雅可比矩阵最直观的理解,一旦理解了,是不是其实很简单呢?
瞬时运动学的这个公式太优美了,让我们再看一遍: $$ \dot{x} = J \dot{q} $$ 这个式子表明了,end effector的速度与joint velocity的关系是线性的!这个式子的形式也与我们在线性代数中用尽了各种方法(高斯消元法是其中一种)去求解的线性方程Ax = b一模一样:如果我们想要end effector以某个速度运动,求对应的关节速度,那这个问题就是一个解线性方程的问题了!比起逆运动学,这实在漂亮方便了不知道多少倍呢。
如果你只知道A矩阵是正方形时怎么解,那么学习机器人学就可以帮助你以最直观的方式了解当A矩阵是瘦高型或者矮胖型的时候是什么意义、又如何求解了——又学机器人学又学线性代数,是不是很超值?下一篇文章,作者会教你如何写出雅可比矩阵,更会带你深入地了解它、应用它(比如我们第一篇干货文就提到的奇异点Singularity和冗余自由度Redundancy,都可以从雅可比矩阵获得数学上的理解),顺便还会教你如何对付高瘦矮胖的线性方程。