所谓的正运动学,英文叫Forward Kinematics或Direct Kinematics,简单来说,就是你知道每个关节的位置(关节位置指平移关节的位移或旋转关节的转角),求末端执行器(end effector)的位置/朝向(position/orientation)。以一个简单的RR平面机械臂的例子介绍:
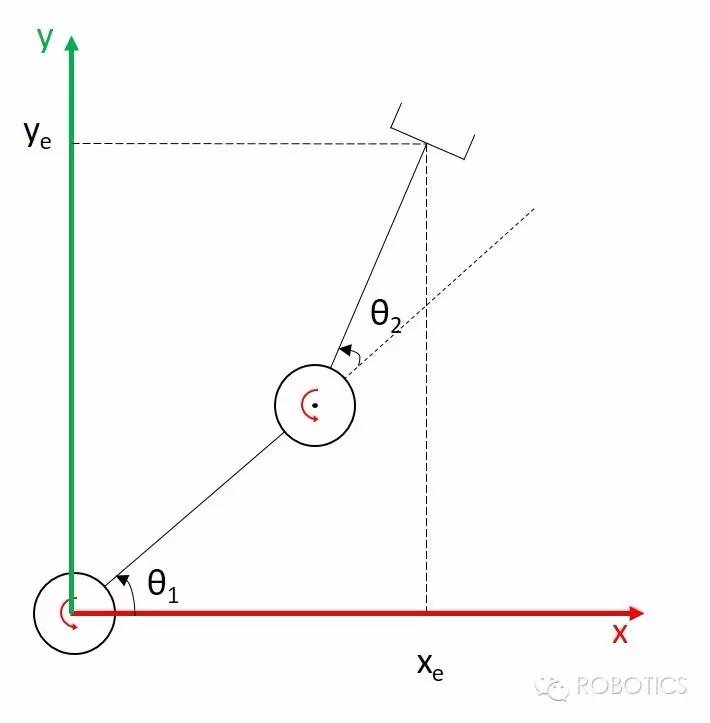
首先,假设我们只关心end effector的位置$(x_e,y_e)$,那么在这样的设定下,关节空间就是$(\theta_1,\theta_2)$,操作空间就是$(x_e,y_e)$。我们的任务是求从关节空间到操作空间位置关系的映射。在上图中,假设每段link的长度为1,则机器人的几何关系直接写出:
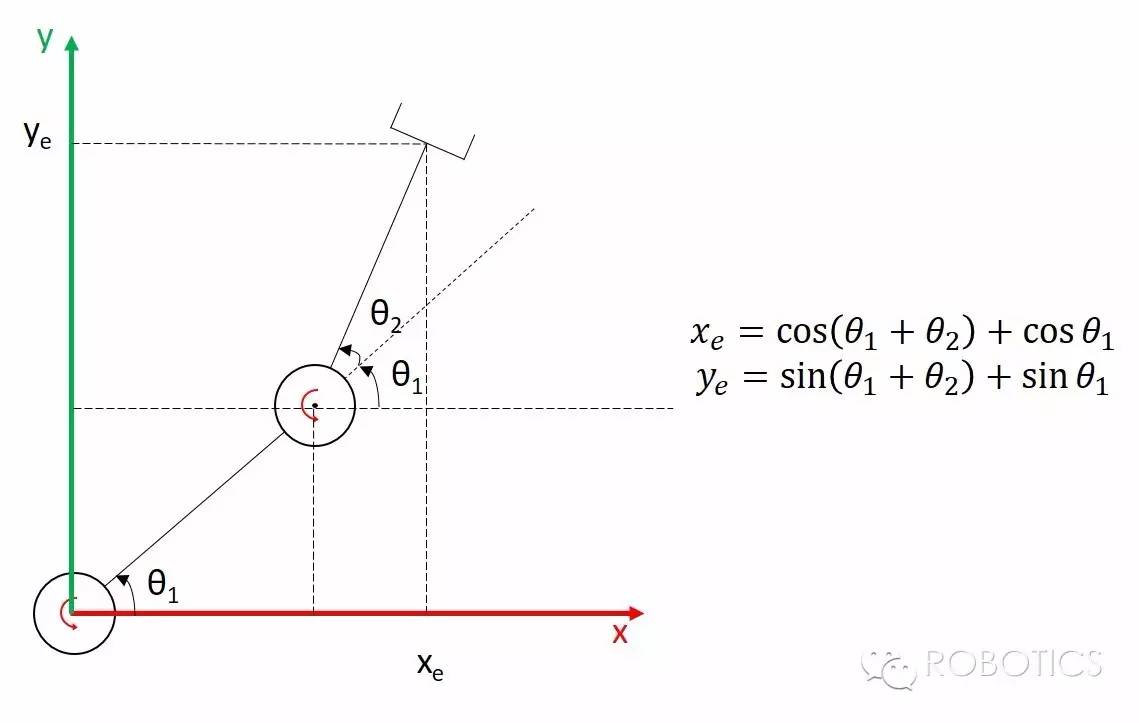
通过$(\theta_1,\theta_2)$求出$(x_e,y_e)$,即为RR机械臂的正运动学。
不过,如果我们有四轴、六轴、甚至更多轴呢?如果我们的end effector操作空间有六个自由度呢?显然,这种情况下简单粗暴的几何法已经超越人类正常大脑的认知了。我们要如何表示这个映射,又要怎么计算呢?
这个时候,我们之前讲到的坐标变换和DH参数就该派上用场了!
对于六自由度的end effector(即操作空间有六个自由度),我们可以重新表述正运动学所解决的问题——那就是,我们需要求end effector的position and orientation相对于base frame、以joint position为变量的坐标变换(函数)。用数学语言描述,就是: $$ \vec {x} = f(\vec{q}) $$ 其中q是关节空间位置向量,就如同上面例子中的$(\theta_1, \theta_2)$;x是操作空间位置和朝向向量,如同上面例子中的$(x_e,y_e)$。由于表示三维的朝向/角度并不容易,我们可以暂且把x理解为end effector的坐标变换矩阵,这样我们就有了这个式子: $$ {}_e^0T=f(\vec{q}) $$ 式子左边表示end effector的坐标w.r.t第0个坐标即base frame(如果你对这样的记法还不熟悉,强烈建议你再看看那篇坐标变换那篇文章)。
我们前面说对于六轴甚至更多轴的机械臂,直接写出这个$f(\boldsymbol {q})$很难。在DH参数那篇文章中,我们详细讲了如何用四个参数(其中一个为关节位置)给每一个关节附上一个坐标系。现在,这些坐标系正好可以帮我们简化求$f(\boldsymbol {q})$的问题: $$ {}^0_eT = {}^0_1T \ {}^1_2T \ \cdots \ {}^{n-1}_{n}T \ {}^n_eT $$ DH参数坐标体系最方便的地方在于,我们可以直接将每一个T矩阵用DH参数表示——在写出这个矩阵之前,我们先复习一下:
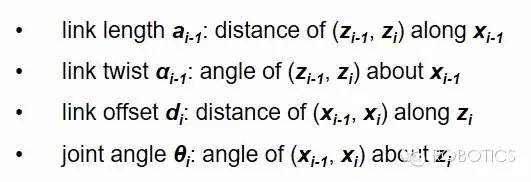
现在我们要求两个有特定关系的坐标之间的坐标变换(一定要结合上一张图看清楚每个变量都是指的哪里)
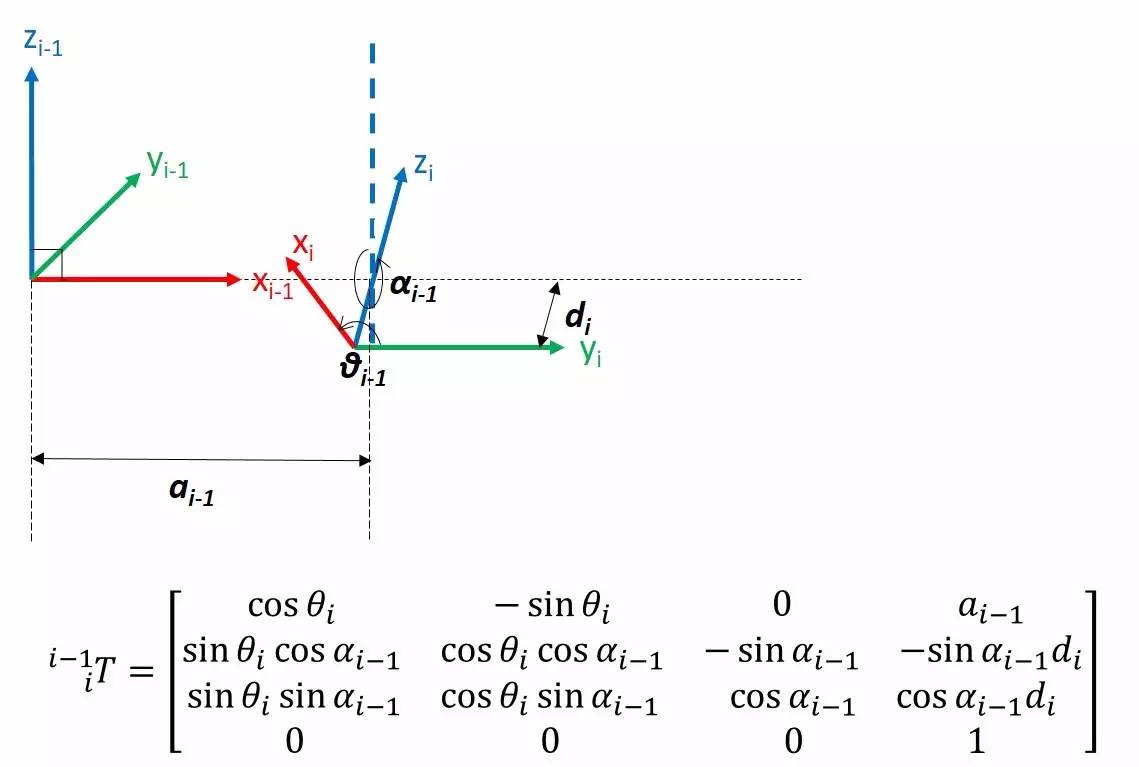
上面这张图和这个公式意味着什么呢?意味着我们可以从每个关节的四个DH参数出发,最后得到一个机械臂的正运动学公式!
需要注意的是,实际应用中在写两个关节之间的T矩阵时,如果坐标系之间关系很简单(DH参数中有很多个0),那我们也常常可以用几何大法解决;至少可以用来凭直觉验证用DH法写出来的矩阵对不对——不要忘了这个重要的工具哦。
以上篇文章讲的RPRR机械臂为例子——记得不管给你什么样的机械臂,不管是要求正运动学解(还是以及以后讲到的逆运动学解、瞬时运动学解、动力学……),第一件事就是给每个关节附上一个坐标系。附坐标系的方法呢,用我们讲的DH参数法通用简洁明了,用你自己的办法也完全可以。
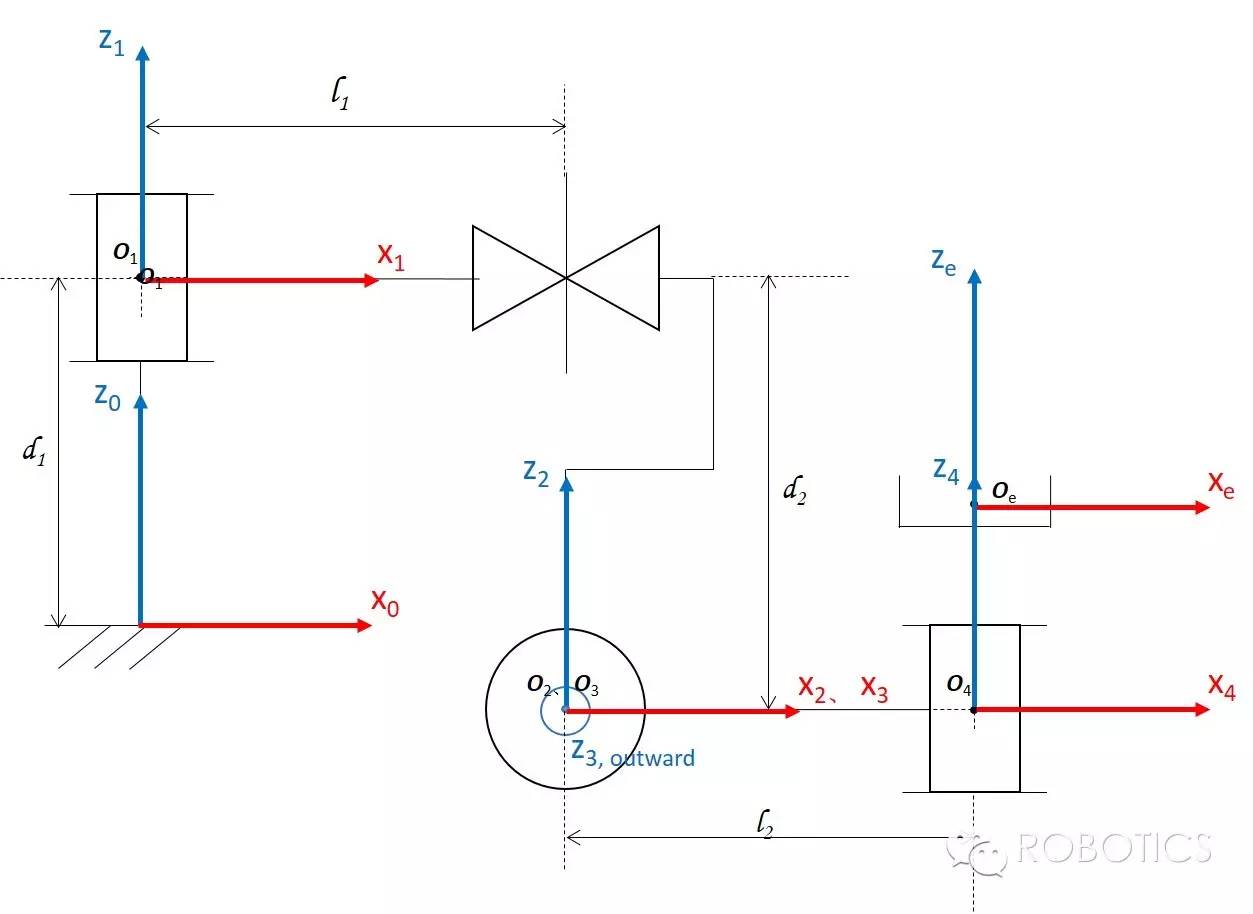
其DH参数表为:
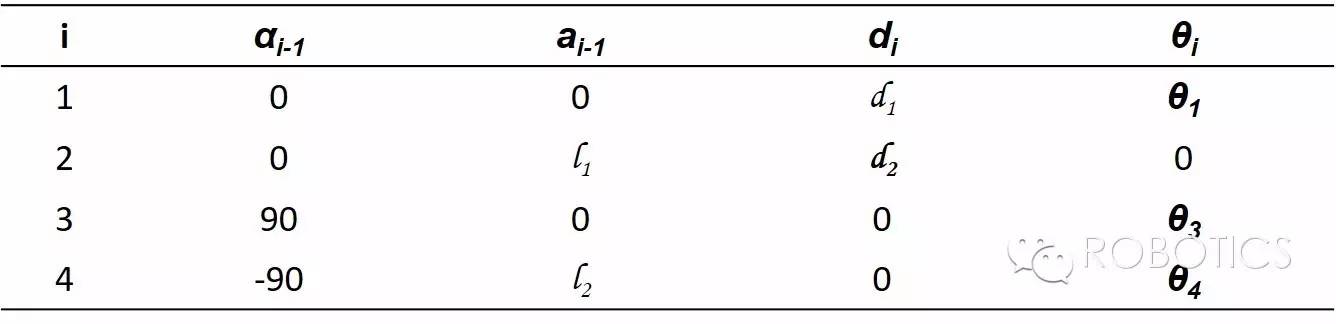
我们现在的任务就是求用关节参数q表示的 end effector w.r.t frame{0}的T矩阵。按照上文提到的方法,我们首先要用几何大法或DH大法把每两个相邻关节之间的T矩阵写出来(实话说,这个机械臂几乎每一个T都可以用几何法直接写出来……如果你清楚地记得旋转矩阵每一列的意义以及T矩阵最后一列平移向量的意义)。
为了方便,我们把cos都写成c,sin都写为s:
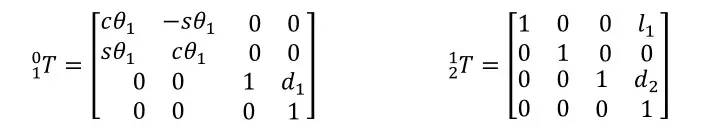

要求end effector的T矩阵,我们还需要一个end effector w.r.t frame{4}的T矩阵;不过这个矩阵非常简单,我就不帮大家写啦。最后,你可以把这些T矩阵都按顺序乘起来,就得到这个机械臂矩阵形式的正运动学解了。有了这个end effector w.r.t frame{0}(frame{0}通常是某个固定于基座的坐标系)的T矩阵,我们就可以从关节位置求得end effector的位置及朝向。
最后想要提的一点是,为什么从关节空间到操作空间就是“正”运动学呢?(相应的从操作空间到关节空间就是“逆”运动学。)因为从q到x的映射是唯一的:同样的q一定对应同样的x。这一点反过来却不成立:同样的x有可能对应不同的q;对于我们在第一篇文章中以人的手臂为例提到的redundant robot来说,同样的x甚至可以对应无数个q。所以,正运动学很简单,逆运动学很麻烦——机器人学有不少的一部分内容,就是在和麻烦的逆运动学作斗争。
正运动学虽然简单,但是它是我们之前两篇文章:坐标变换与DH参数的第一次结合。如果你想要学习机器人学,一定、一定把这两篇基础文章都弄清楚。
这篇文章就这么愉快地结束啦!