今天我们要讲所有学习机器人学的人都需要具备的一项基本技能——坐标变换。看明白这篇文章,你需要一点基础的向量和矩阵知识,不用多,只要知道向量的加减,点乘(内积);矩阵的定义、加减乘逆以及转置;还有矩阵与向量的乘法就够了。
机器人学为什么需要坐标变换呢?因为控制一个机械臂的根本,就是弄明白每一个关节的joint position与end effector的position and orientation的关系,用更简洁的话来讲,就是joint space与operational space之间的互相映射关系。这里有两个小说明:
-
不仅仅是位置/角度的映射关系,也包括速度、加速度、力或扭矩的映射关系
-
所有直接用英文而没有翻译的词汇,都是在第一篇文章中解释过的重要概念
1 坐标系(coordinate system)
描述空间位置、速度和加速度,大部分都是用笛卡尔坐标系,也就是大家熟知的三个互相垂直的坐标轴组成的坐标系。我只想强调几个地方:
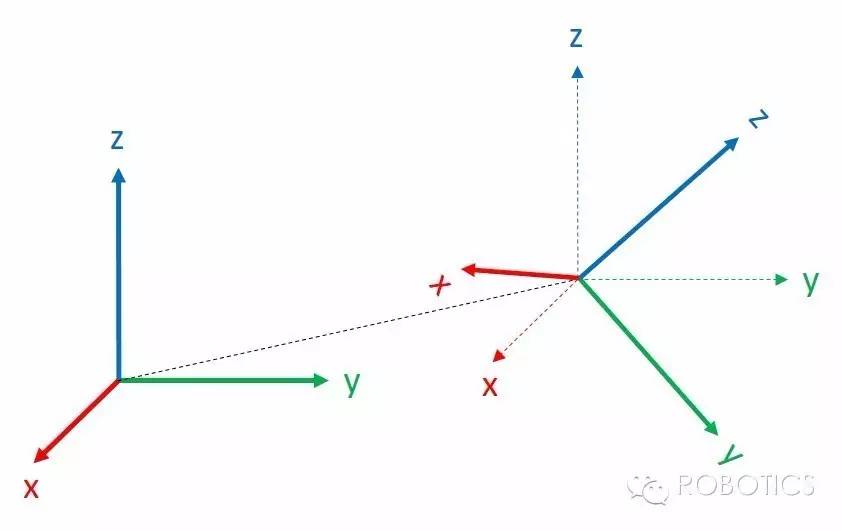
- 像题图那样的彩色坐标系,若无特别说明,都是rgb(红绿蓝)依次对应xyz
- 当我们说绕某一个轴旋转多少角度时,正方向的确定用右手定则,如下图:
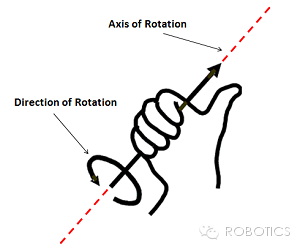
- 我们用的都是右手坐标系,即绕z轴旋转时,y轴在x轴的+90度方向(注:逆时针为正方向)
- 提到某一个坐标系,比如坐标系A时,我们说frame{A},用大括号表示
- 提到任意需要指明参照系的量时,我们将坐标系写在左上角,如坐标系{A}中点P的位置向量写作${^A}P$
- 我们将物体/点的名称写在右下角,如坐标系{A}中点O的位置向量写作$^Ap_O$
- 提到一个量是相对于某个坐标系时,比如{A},我们说with respect to {A},或简写为w.r.t {A}。
- 本文及以后的文章中所有向量都是列向量,所有向量的转置都是行向量
- 以上是一套比较常用的标记系统(convention),始终遵循同一套convention有助于在混乱的坐标变换中找到清晰的思路;如果你已经有常用的记法,那么保持你自己的记法也是可以的
2 位置(position)、平移变换(translation)
位置是最简单的,用一个三维向量来表示,想必不用多讲。唯一需要注意的是,讨论一个位置向量一定要指明参照坐标系。
平移变换是坐标系空间位置的变换,可以用坐标系原点O的位置向量表示,如图所示。多次平移变换也很简单,直接向量相加就可以了
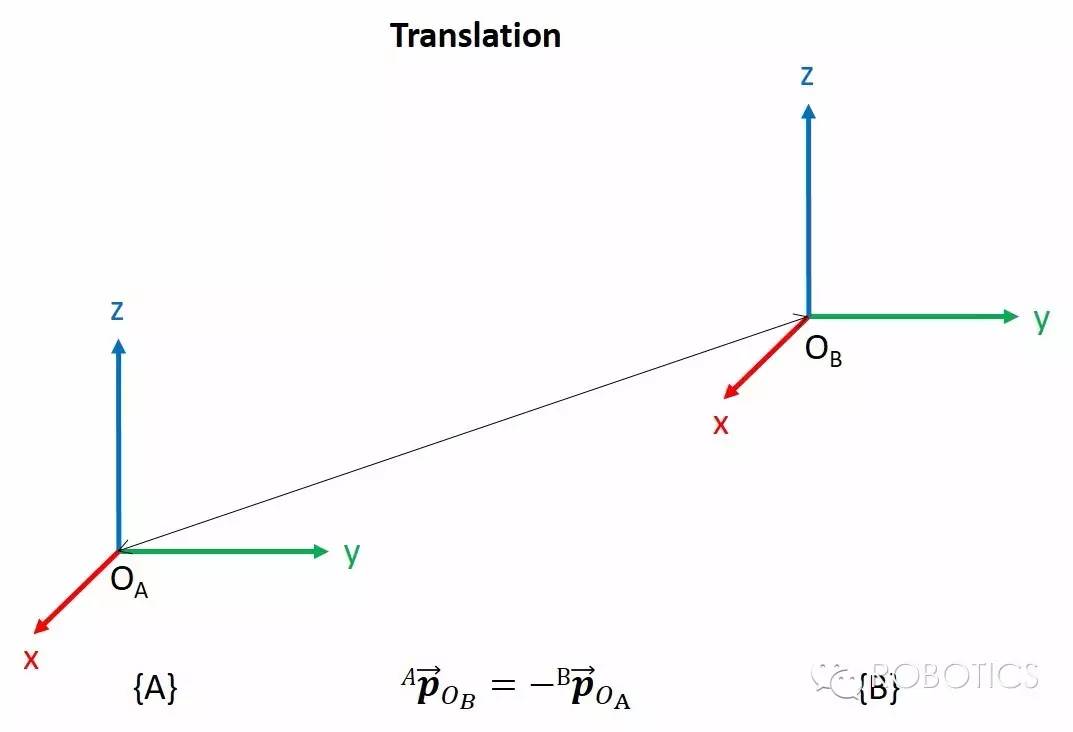
求空间中一个点的位置在经过平移变换后的坐标系B中的坐标(point coordinate with respect to frame{B}),看图很快就能明白,就不多讲了。
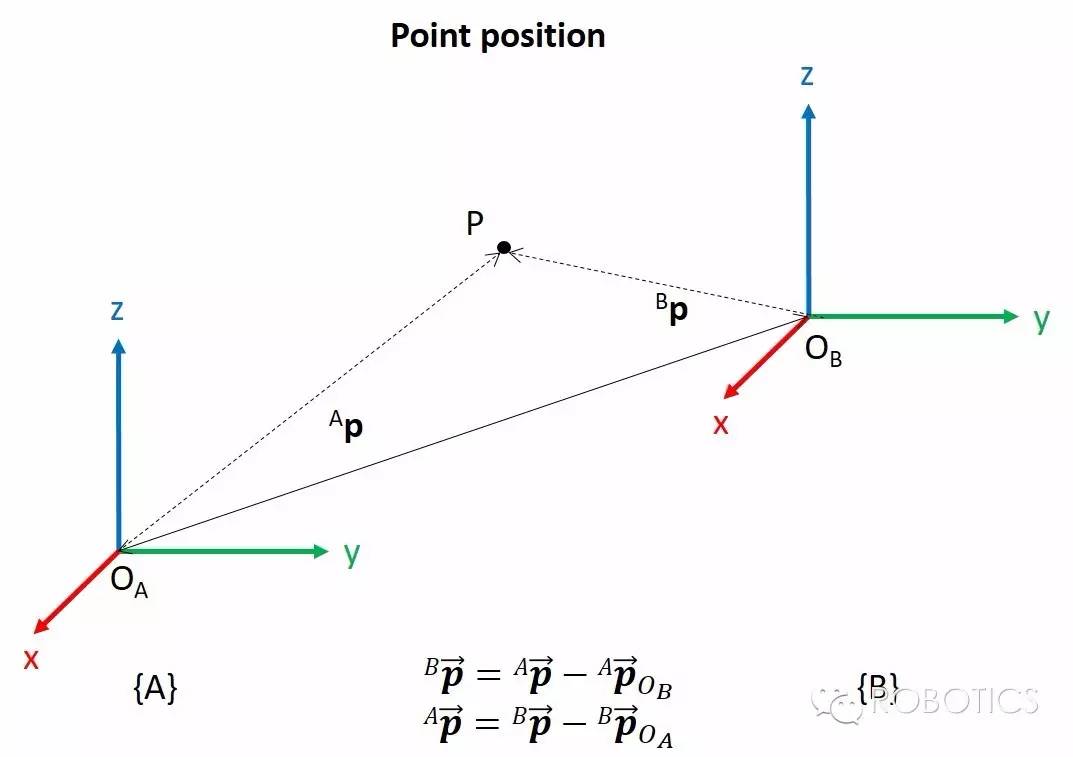
3 角度/方向(orientation)、旋转变换(rotation)
相比于位置,Orientation的表示方法就麻烦多了。在讨论Orientation之前,有必要说明一点:要表示一个物体的三维位置和朝向,我们通常都在物体上“附上”一个跟着它动跟着它转的坐标系(attach a frame to the object),然后通过描述这个坐标系与参考坐标系的关系来描述这个物体。所以,描述一个物体在坐标系中的位置和朝向,总是可以等效为描述坐标系之间的关系。因此我们这里讲角度/方向表示法,只要讲两个坐标系之间的关系就可以了。
要知道一个坐标系相对于另一个坐标系如何旋转、旋转了多少,应该怎么做呢?我们先从二维的情况看起:
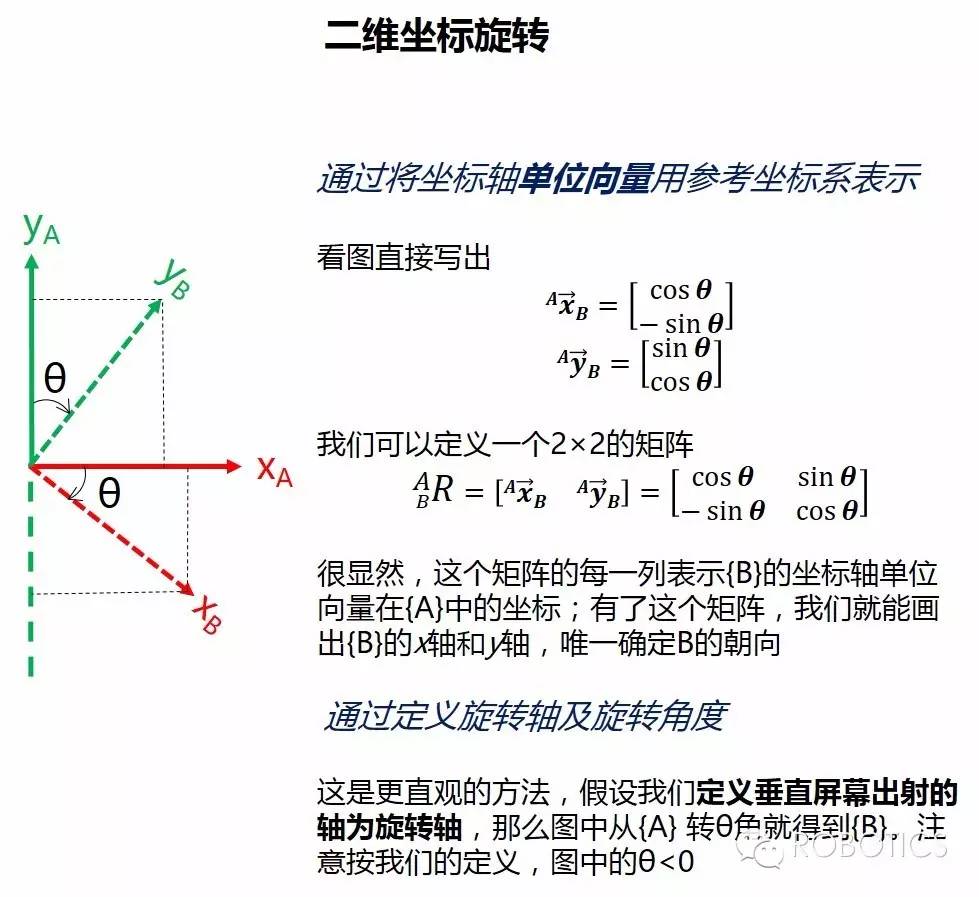
希望对你来说上图可以轻易看懂:),因为我们需要在它的基础上扩展到三维的情况
3.1 旋转矩阵
空间三维朝向相对来讲复杂得多,因为平面上坐标的朝向只能有一个自由度,即绕垂直平面的轴旋转;而空间中物体的朝向会有三个自由度。不过,如果我们从上图的第一种方法出发,就可以轻松写出一个3×3的R矩阵,我们叫它旋转矩阵(Rotation matrix): $$ {}^A_BR=[{}^A\vec{x}_B \quad {}^A\vec{y}_B \quad {}^A\vec{z}_B] $$ 这个式子太重要了!它表明从{B}到{A}的旋转矩阵的每一列都是{B}的坐标轴单位向量在{A}中的表示(wrt {A})。很多人可能用旋转矩阵进行各种计算,却始终弄不清楚它的物理意义是什么。记住一个R矩阵究竟表示什么,很多情况下你甚至可以轻松写出它来:
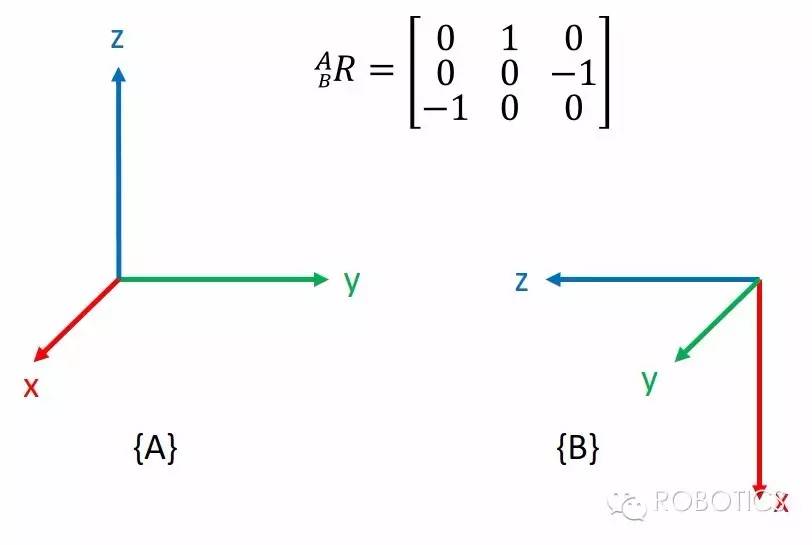
看明白没?
从这个式子出发,我们可以很快发现旋转矩阵的很多神奇之处,比如它是一个正交矩(orthonormal matrix,不仅正交,且每一行每一列的长度都为1),这意味着它的转置等于求逆:
由
$$ ^A_BR = [{^A}\vec{x}_B \quad {^A}\vec{y}_B \quad {^A}\vec{z}_B] $$
可得
$$
{}^A_BR^T = \begin{bmatrix}
{}^A\vec{x}^T_B \\
{}^A\vec{y}^T_B \\
{}^A\vec{z}^T_B
\end{bmatrix}
由于坐标轴正交且为单位向量
$$
$$
\begin{align}
{}^A_BR^T {}^A_BR & = \begin{bmatrix}
{{}^A\vec{x}_B}^T \\
{{}^A\vec{y}_B}^T \\
{{}^A\vec{z}_B}^T
\end{bmatrix}
[{}^A\vec{x}_B \quad {}^A\vec{y}_B \quad {}^A\vec{z}_B] \\
& = \begin{bmatrix}
{{}^A\vec{x}_B}^T {}^A\vec{x}_B & {{}^A\vec{x}_B}^T {}^A\vec{y}_B & {{}^A\vec{x}_B}^T {}^A\vec{z}_B \\
{{}^A\vec{y}_B}^T {}^A\vec{x}_B & {{}^A\vec{y}_B}^T {}^A\vec{y}_B & {{}^A\vec{y}_B}^T {}^A\vec{z}_B \\
{{}^A\vec{z}_B}^T {}^A\vec{x}_B & {{}^A\vec{z}_B}^T {}^A\vec{y}_B & {{}^A\vec{z}_B}^T {}^A\vec{z}_B
\end{bmatrix} \\
& = \begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{align}
$$
注意$x^Ty$就是向量的内积/点乘。
旋转矩阵将一个坐标系旋转为另一个坐标系,那么不难理解旋转矩阵的逆亦即转置可以将坐标系旋转回来。根据上面那个极其重要的式子,可以很快想到矩阵的每一行就是{A}的坐标轴在{B}中的表示。因此,我们可以将这个式子扩展如下:
$$
{}^A_BR = [{}^A\vec{x}_B \quad {}^A\vec{y}_B \quad {}^A\vec{z}_B]
= \begin{bmatrix}
{{}^B\vec{x}_A}^T \\
{{}^B\vec{y}_A}^T \\
{{}^B\vec{z}_A}^T
\end{bmatrix}
= {{}^B_AR}^T
$$
3.2 欧拉角(Euler angles)、转轴转角(Angle-axis)表示法、四元数(Quaternion)
我们说空间中的旋转有三个自由度,因此旋转矩阵是非常冗余的(9个数)。在上面二维坐标旋转的图中,除了用旋转矩阵,我们也用一个角度来表示旋转——三维的情况也类似,你总可以通过定义旋转轴和转角的方式来表示坐标系的朝向或旋转变换。Euler angles, Angle-axis和Quaternion都是常用的基于旋转轴和旋转角的旋转表示方法,其中前两种用三个变量表示,Quaternion用四个变量表示。Quaternion用一个冗余的变量解决了其余两种表示方法无法避免的Singularity问题,在运算插值时也比较方便,因此是计算机程序中表示旋转最常用的一种表示方法。
由于这部分内容比较多也比较复杂,我会在合适的时候专门用一篇文章详细介绍。
现在还是让我们回到旋转矩阵。求空间中一个点的位置在经过旋转变换后的坐标系A中的坐标,可以用旋转矩阵解决——因为空间中每个点的位置都是坐标轴单位向量的线性组合。
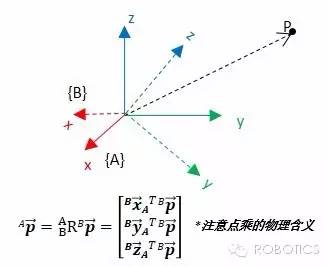
我们说连续的平移变换只需要向量相加,那么连续的旋转变换呢?只要矩阵相乘就可以了:
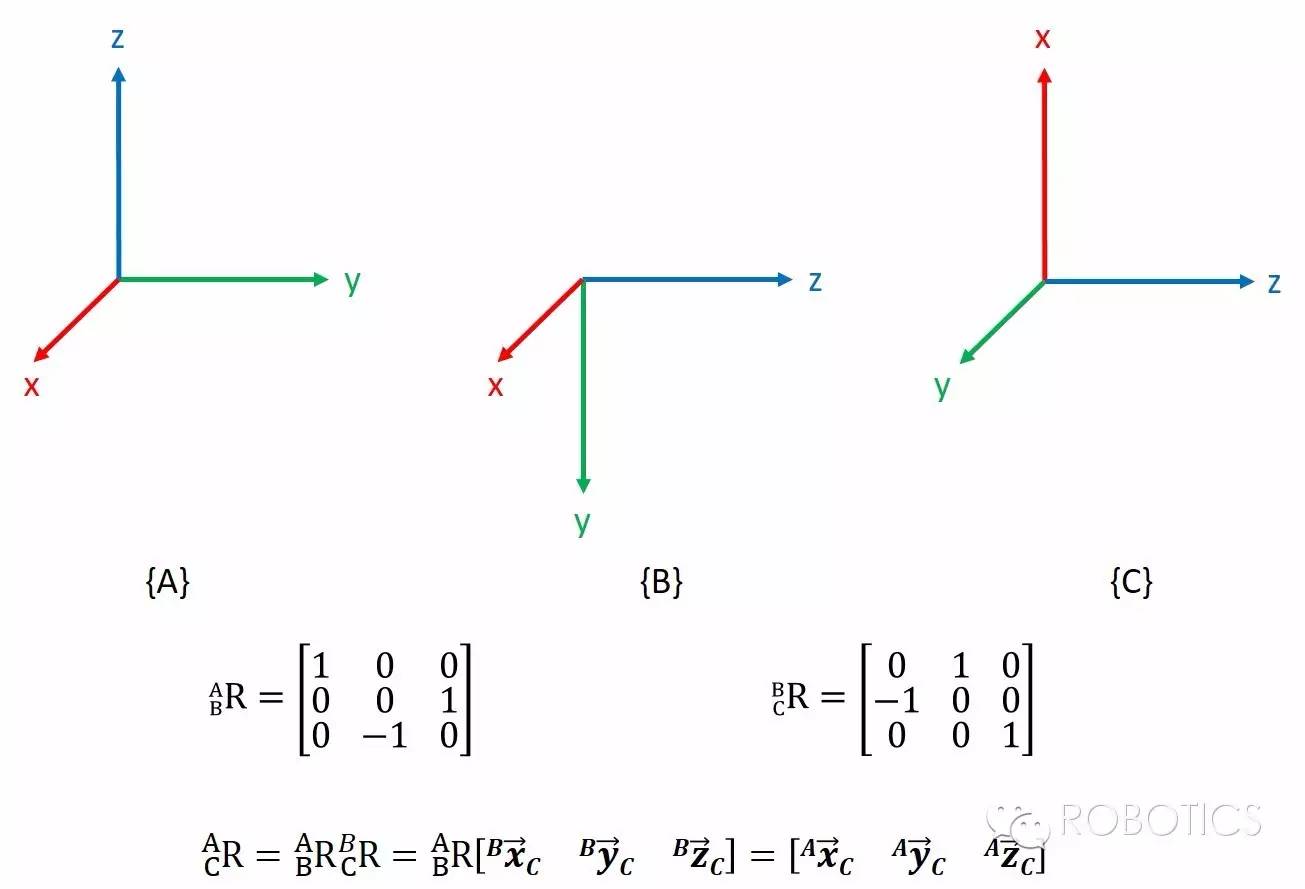
看了这么多旋转矩阵,你一定明白我们始终把参照坐标系写在左上角的原因了;如果你不坚持用一种convention,那么你很快就会迷失在坐标变换的汪洋大海中…
4 齐次坐标变换(homogeneous transformation)
有了平移和旋转,我们就可以来讲齐次坐标变换了。首先试想,求空间中一个点在经过平移+旋转变换的坐标系中的坐标应该怎么求呢?最直观的想法,可以先平移再旋转:
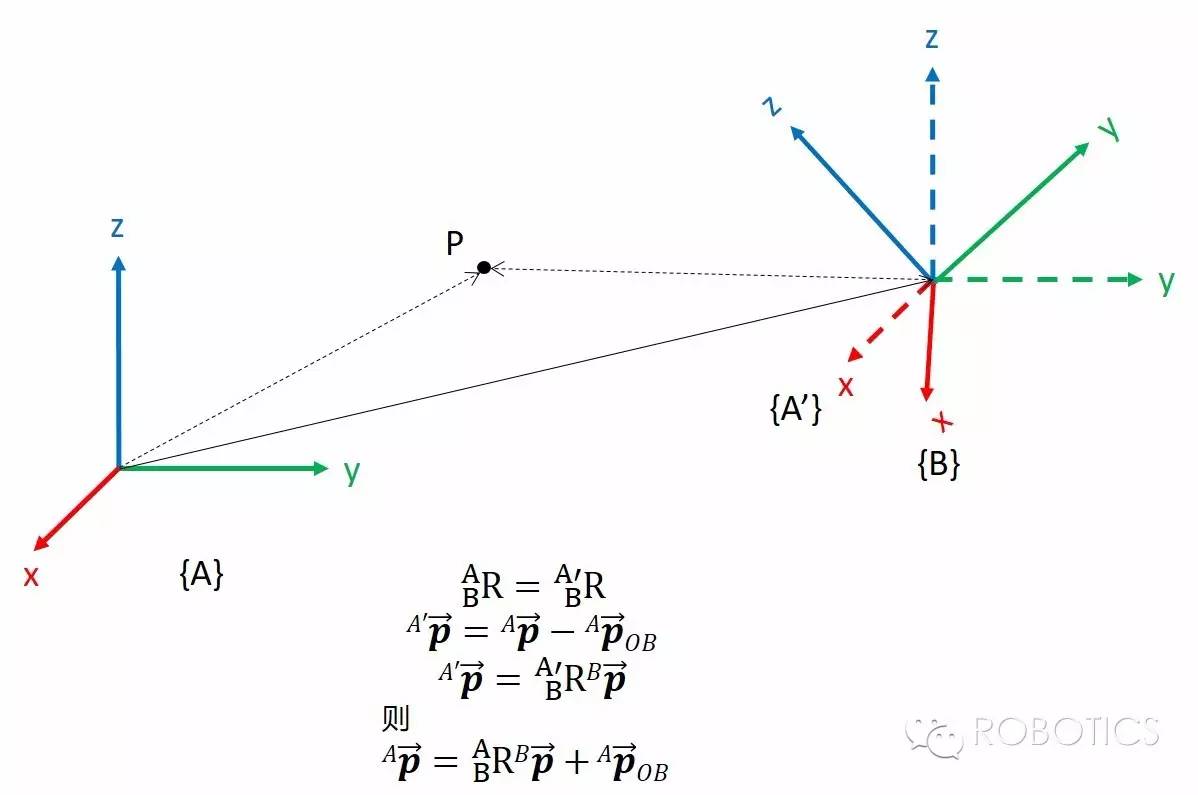
你可能会想,那我能不能把这整个过程用一个矩阵表示呢?齐次坐标变换矩阵(Transformation matrix)就是为了这个目的:
$$
{}^A_BT = \left[
\begin{array}{c|c}
{}^A_BR & {}^A\vec{p}_{OB} \\ \hline
0 \quad 0 \quad 0 & 1
\end{array}
\right] \\
\begin{bmatrix}
{}^A\vec{p} \\
1
\end{bmatrix} = {}^A_BT \begin{bmatrix}
{}^B\vec{p} \\
1
\end{bmatrix}
$$
相信你可以看出上面两张图的式子其实是一样的,只不过第二张图表示成了T矩阵的形式。
T矩阵在一个4×4的矩阵中同时表示旋转变换和平移变换,它方便了坐标变换的逆运算、多坐标系的连续变换;规则与旋转矩阵类似: $$ {}^B_AT = {}^A_BT^{-1} = \left[ \begin{array}{c|c} {{}^A_BR}^T & -{{}^A_B}R^T \cdot {}^A\vec{p}_{OB} \\ \hline 0 \quad 0 \quad 0 & 1 \end{array} \right] $$
建议你自己尝试推导。
5 小结
这篇文章主要讲解的概念有:
- 坐标系(coordinate system)
- 平移变换(translation)
- 旋转变换(rotation)
- 齐次坐标变换(homogenous transformation)
注:永远可以把坐标系中一个点的旋转平移,等效为坐标系本身相反方向的旋转平移